Kur viešpatauja chaosas? Vartiklis

Prieš 50 m. susiformavo nepaprasta teorija. 1963 m. „Journal of Atmosferic Sciences“ kovo mėnesį išspausdinta kažkas neįtikėtina – Edward Lorenz‘o¹⁾ straipsnis „Deterministinis neperiodinis srautas“ apie gamtos reiškinių nuspėjamumą. O atradimui pastūmėjo grynas atsitiktinumas.

1961 m. pradžioje E. Lorencas modeliavo atmosferos sistemas. Tuo metu dauguma oro prognozių buvo rengiamos ekstrapoliuojant ankstesnius stebėjimus su minimaliu atmosferos fizikos pritaikymu. Lorencas bandė suvokti, kiek nuspėjami oro procesai, tad sudarė supaprastintą lygčių sistemą, aprašančią oro judėjimą atmosferoje (konvenciją), o jų sprendimui panaudojo „Royal McBee“ kompiuterį LGP-30.

Proveržis įvyko jam MIT‘e susidomėjus vieno iš paskaičiavimų eiga. Sustabdęs kompiuterį, jis įvedė tarpinius duomenis iš ankstesnio paskaičiavimų etapo, paleido programą ir išėjo išgerti kavos. Grįžęs pamatė, kad paskaičiuota oro dinamika už du mėnesius, tačiau naujas sprendinys nesutapo su ankstesniu. Palyginęs paskaičiavimus pastebėjo, kad nors pradžioje duomenys buvo artimi, vėliau jie ėmė smarkiai skirtis.

Netrukus išaiškėjo, kad skirtumai kilo dėl apvalinimo klaidos: kompiuteris spausdino skaičius iki 6-o ženklo po kablelio, o Lorencas juos įvesdamas apsiribojo trimis skaitmenimis po kablelio. Nežymių skirtumų pakako, kad būtų gauti visiškai kitokie rezultatai. Jautrumo pradiniams duomenims problema tapo labai nemaloni užsiimantiems prognozėmis...

Tyrinėtojai ir anksčiau buvo atkreipę dėmesį į galimą priklausomybę nuo pradinių duomenų, tačiau neįvertino pasekmių masto. Prieš šimtmetį Anri Puankarė parodė, kad trijų dangaus kūnų judėjimo negalima aprašyti paprastomis formulėmis. Lorenco atraktorius

O jo mokinys Žakas Adamaras (Jacques Hadamard) įrodė, kad trajektorijas abstrakčiuose matematiniuose paviršiuose, pvz., dvigubame tore, sunku numatyti. Parodęs, kad realios sistemos sunkiai prognozuojamos, Lorencas sugebėjo sujungti visas ankstesnes idėjas.

Iš jo atradimo sekė galimas stebimų oro šablonų (tipų, režimų) paaiškinimas. Jį jau senokai domino, kodėl vienos konfigūracijos įvyksta dažniau už kitas. is kompiuteriniuose modeliuose pastebėjo, kad oro dalelių trajektorijos artėja prie atraktoriaus – pritraukiančios aibės, panašios į supainiotas dvimates spirales. Tai rodo, kad sistema vienu metu gali būti ir nenuspėjama, ir turėti elegantišką tvarką. Ir, nors pritraukę meteorologų dėmesį, Lorenco mintys tik po dešimtmečio ėmė daryti įtaką kitoms mokslo sritims.

Matematikas James Yorke visad su savimi nešiojosi bloknotą, kuriame užrašinėjo uždavinių sprendimus. 8-o dešimtm. pradžioje vienu tokių buvo lygtis, iš pirmo žvilgsnio duodanti nenuspėjamus rezultatus. Kaip ir Lorenco atveju, ji buvo ir labai jautri pradinėms reikšmėms, ir labai stabili – visi taškai galiausiai patekdavo į tą patį atraktorių. Jorkas tokias lygtis pasiūlė pavadinti chaotinėmis, nes jų sprendiniai nuspėjami tik teoriškai, o ne praktiškai. Vėliau Lorencas išsireiškė, kad chaosas – tai „kažkas atrodančio atsitiktiniu, bet ne atsitiktinis“.

Tuo metu chaoso teorija patraukė kitų sričių tyrinėtojus, tarp jurių buvo ir Robert May⁹⁾, biologas iš Prinstono un-to. Jis spėjo, kad kai kurios paprastos lygtys, naudojamos ekosistemos tyrimams, gali duoti sudėtingesnius nei iki tol manyta rezultatus. Jis aptiko, kad net paprasčiausias populiacijos modelis, loginio atvaizdavimo funkcija, gali pasireikšti chaotine elgsena.

Paaiškėjo, kad biologinės sistemos gali vystytis labai sudėtingais keliais, nepriklausomai nuo labai paprastų taisyklių rinkinio. Tapo aišku, kad politikai ir ekonomikai irgi turi suprasti, kad paprastos sistemos gali vystytis visai ne paprastai.

Tuo pat metu IBM tyrimų centre Benoit Mandelbrotas tyrinėjo kitus gamtos struktūrų tipus. Tarp jų jį labiausiai sudomino fraktalai. Jis aptiko, kad pasaulis pilnas fraktalų: nuo lapų iki bronchų plaučiuose, nuo debesų iki kranto linijų.

1979 m. jis stažavosi Harvardo un-te ir tą laiką skyrė fraktalų studijoms. Jis dėmesį sutelkė į Julia aibę, kuri apie 60 m. nieko nesudomino. Pradžioje patrypčiojęs vietoje, paskaičiavimams panaudojo kompiuterį ir pasirodė nepaprastos figūros. Jose Mandelbrotas įžvelgė kažką pažįstamo. Tasai siurrealistinis žmogaus sukurtas vaizdas atrodė nepaprastai natūraliu – ir plačiai išgarsėjo. Mandelbroto darbai padėjo išsiaiškinti ir

Kai Lorencas apie savo atradimą papasakojo kolegoms, vienas jų replikavo, kad, jei teorija teisinga, tai žuvėdros sparnų mostas gali visiems laikams pakeisti orus. Šios metaforos žuvėdra pamažu transformavosi į labiau poetišką drugelį, ir jau po kelių metų pats Lorencas konferencijos metu klausė: „Ar drugelio sparnų mostas Brazilijoje gali sukelti uraganą Teksase?“ (matyt, įtakotas R. Bredberio apsakymo „Ir nugriaudė griaustinis“). „Drugelio efektas“ (žr. ir >>>>>) tapo sparnuotu posakiu, nusakančiu stiprią priklausomybę nuo pradinių sąlygų.

evoliucijos klausimus. Nuo Darvino laikų naudotas „aklo laikrodininko principas“ pagrindimui, kad pasaulis neevoliucionavo natūraliai, o buvo sukurtas. Atseit, tarsi kišeninis laikrodis, gamta yra pernelyg sudėtinga, kad atsirastų be protingo kūrėjo. Tačiau paaiškėjo, kad sudėtingi dalykai gali kilti iš paprastų taisyklių.

Du dešimtmečius chaoso teorija dominavo biologijoje. Bet tik 2008 m. rastas patvirtinimas, tenkinantis chaoso apibrėžimą pagal Jorką, Amsterdamo un-to tyrinėtojų gautas po 6 m. trukusių planktono tyrimų. Pastebėta, kad planktono populiacija jautri pradinėms sąlygoms (neįmanoma prognozuoti ilgesniam nei 15-30 dienų laikotarpiui) ir kartu labai stabili (rastas atraktorius).

Fizikams buvo paprasčiau. Iš esmės, jie jau buvo susidūrę su chaotine elgsena, pvz., neono lempose ir elektros grandinėse, tik į tai nekreipė dėmesio. Paskelbus chaoso teoriją, fizikai ėmėsi jo ieškoti ir kitose srityse. Buvo žinoma, kad plokščiame inde su skysčiu pašildžius dugną kyla sudėtingai nusakomos srovės. Bet tik 1978 m. prancūzas Albert Libchaber‘is¹⁰⁾ įrodė, kad dėl to kaltas chaosas. Tačiau iki šiol neaiškus turbulencijos reiškinys – ir už šio uždavinio sprendimą Klėjaus institutas skyrė milijono dolerių premiją.

Chaoso teorija iškelia ir naujus klausimus. Vienas jų susijęs su savireguliacija. Kodėl chaotinių sistemų dalyviai staiga „sinchronizuojasi“?

Naujas lakmusas chaosui patikrinti?

Ar gali drugelio sparnų mostas Brazilijoje sukelti tornadą Teksase? Tai vadinamasis „drugio efektas“, plačiai naudojamas chaotinių sistemų koncepcijos iliustracijai – kad maži pokyčiai pradinėse sąlygose gali sukelti visai kitokią sistemos elgseną.

Chaoso supratimas ir modeliavimas gali padėti išspręsti daugelį mokslinių ir inžinerinių problemų, tad ieškoma naujų chaoso apibrėžimų. Neseniai Merilando un-to tyrėjai pateikė platesnį už ankstesnius chaoso apibrėžimą. Jis kompaktiškas, gali būti lengvai pritaikytas skaičiavimo metodams ir tinka plačiai chaotinių sistemų įvairovei – nuo medicinos iki meteorologijos ir kt. Chaotiškas elgesys
[publikacija 2015 m. liepos 28 d. „Chaos“ žurnale]

Matematiškai išskirtinis jautrumas pradinėms sąlygoms gali būti atvaizduotas Liapunovo eksponente. Jos reikšmė teigiama, jei dvi be galo artimos pradinės reikšmės diverguoja laikui bėgant. Tačiau Liapunovo eksponentė duri apribojimų jos panaudojimui kaip chaoso apibrėžimą: ji leidžia tik patikrinti chaoso buvimą tam tikrame modelio sprendime bey ne patį modelį; ir ji gali būti teigiama net tada, kai modelis yra per daug stabilus, kad atrodytų kaip chaotinis.

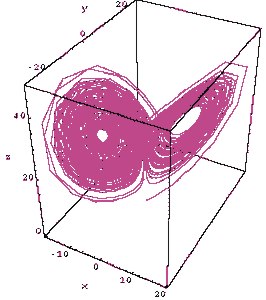
Įdomu, kad chaotinis Lorenco lygčių sprendinys atrodo tarsi du peteliškės sparnai (žr. iliustraciją aukščiau). Ši forma matematiškai apibūdinama kaip atraktorius (pritraukianti), kas reiškia, kad ją lengva identifikuoti su Liapunovo eksponente. Tačiau ne visos chaotinės elgsenos tokios aiškios. Pvz., paimkime 4 Kalėdų eglutės stiklinius burbulus sustatytus į piramidę. Šviesos spindulys atsispindi nuo jų į visas puses. Daugumos šviesos kelias tiesus, tačiau kai kurie fotonai gali būti „įkalinti“ piramidėje, chaotiškai šokinėdami tarp burbulų. Šie chaotiški keliai matematiškai apibūdinami kaip repeleriai (atstumianti) ir yra sunku jiems rasti modelį. Repeleriai dažnai sutinkami fizikinėse bei gamtos sistemose, pvz., vandentiekio tinkluose, asteroidų orbitose, cheminėse reakcijose, paukščių būriuose ir pan.

B. Huntas¹¹⁾ ir E. Otas¹²⁾ iš Merilando un-to pasinaudojo entropijos koncepcija. Kintančiose sistemose entropija nusako kaip greitai jose susidaro betvarkė ir nenuspėjamumas. Tačiau standartinius entropijos apibrėžimus (metrinės ar topologinės) sunku pritaikyti skaičiavimams, o dar sunkiau daugeliui fizikinių ir biologinių sistemų. Tad B. Huntas ir E. Otas įvedė lankstesnį besiplečiančios entropijos apibrėžimą lengviau pritaikomą realistiškesniems modeliams. Jiedu išplėtė ir chaoso apibrėžimą įtraukdami sistemas, kurias vystymosi metu veikia išoriniai veiksniai. Ir jį nesunku pritaikyti kompiuteriniams paskaičiavimams.

Pvz., dvi identiškos chaotinės sistemos su skirtingomis pradinėmis sąlygomis gali vystytis visiškai skirtingai, tačiau sistemas veikiant išorine jėga jos gali pradėti sinchronizuotis. Pritaikius besiplečiančios entropijos chaoso apibrėžimą ir nustatydami, ar originalios sistemos atsako chaotiškai į poveikius, tyrinėtojai gali pasakyti, ar jie turi kokį nors chaotinės sistemos valdymą. Toks valdymas, pvz., gali būti pritaikytas kuriant labai saugias komunikacines sistemas ir efektyvesnius širdies stimuliatorius.

„Nedideli pradinių sąlygų skirtumai sukelia milžiniškus skirtumas galutiniam reiškiniui... Prognozė tampa neįmanoma“, A. Puankarė

Dar 1950-ais A. Tiuringas pastebėjo: „Vieno elektrono pasislinkimas viena milijardine centimetro dalimi kažkuriuo momentu gali sukelti skirtumą, ar žmogus po metų žus nuo lavinos, ar nuo jos pabėgs“. Ir vaikiškoje Norton Juster’io²⁾ knygelėje „Netikra būdelė mokesčiams“ (1961) Grynojo proto princesė ištaria: „...viską, ką darome, turi įtakos viskam ir visiems, net jei ir menkiausiu būdu. Kodėl, kai musė mosuoja sparnais, vėjas aplekia aplink visą pasaulį“.

1961 m. L. Lorencas MIT’e vykdė orų prognozės kompiuterinį modelį. Jis iš naujo įvedė ankstesnio paskaičiavimo vieno etapų duomenis ir nustebo, kad gautas sprendinys nesutapo su ankstesniu, o vėliau aplamai ėmė žymiai skirtis. Paaiškėjo, kad tai dėl tarpinių rezultatų spausdinimo juos apvalinant. Šie nežymūs tarpinių reikšmių pakitimai sukėlė reikšmingus tolimesnių skaičiavimų pakitimus.

E. Lorencas nebuvo girdėjęs apie „Ir nugriaudė griaustinis“ ir dar nuo 1963 m. („J. of the Atmospheric Sciences“ straipsnyje „Deterministinis neperiodinis srautas“) naudojo žuvėdros sparnų mosto metaforą, tačiau „American Association for the Advancement of Science“ konferencijos 1972 m., kuriai jis pateikė pranešimo tezes, vienas organizatorių (Philip Merilees³⁾, o jį pasiūlė greičiausiai Douglas Lilly⁴⁾ , prisimindamas George R. Stewart’o⁵⁾ romaną „Audra“, 1941) pakeitė jų pavadinimą į „Ar gali drugelio sparnų plazdenimas Brazilijoje sukelti tornadą Teksase?“, nors irgi sakėsi nebuvo įtakotas R. Bredberio apsakymo Ir nugriaud4 griaustinis.

Tiesa, L. Lorencui tasai išsireiškimas turėjo kitokią prasmę. Jis nagrinėjo diferencialines lygtis, aprašančias atmosferos būseną, ir aptiko, kad globalaus klimato matematinis modelis turi du keistus atraktorius, aplink kuriuos grupuojasi daliniai sprendiniai. Be to sistema geba visiškai nenuspėjamai šokinėti nuo vieno atraktoriaus prie kito (pvz., nuo įprastinio klimato prie ledynmečio ir atgal) esant visai nežymiems pradinių parametrų pakeitimams. Iliustracija, parodanti abi sprendinių sritis, dėl savo charakteringos formos buvo pavadinta „Lorenco drugeliu“ (taip pat žr. >>>>>).

Tačiau pats „drugelio efekto“ terminas nebuvo naudotas iki pat 1984 m., kai pasirodė H.G. Schuster’io⁶⁾ knygoje „Deterministinis chaosas“. O knygoje „Chaoso esmė“ (1993) pats L. Lorencas jo esmę apibūdino taip: „Reiškinys, kad dėl nedidelio dinaminės sistemos būsenos pakeitimo vėlesnės būsenos labai skirsis nuo būsenų, kurios būtų buvusios be to pakeitimo“. Tiesa, skirtingose vietose buvo minimos skirtingos geografinės lokacijos.

Vis tik reikia priminti, kad pasekmių jautrumas pradinėms sąlygoms (ir sekantis „domino efektas“) minimas jau daugelyje ankstesnių šaltinių, pvz. 1898 m. V.S. Franklino⁷⁾ recenziją P. Duhemo⁸⁾ veikalui („žiogo stryktelėjimas Montanoje gali nukreipti audrą nuo Filadelfijos į Niujorką“) ar net brolių Grimų pasakoje „Utėlė ir blusa“ (publikuota 1812 m.), kurioje utėlės apsidegimas verdančiu alumi sukelia tvaną. Bet jau „Žmogaus pašaukime“ (1800) J. Fichtė (1762-1814) pastebėjo: „negalite pašalinti nė vieno smėlio smiltelės iš jos vietos, tuo pačiu … nepakeitę kažko visose neišmatuojamos visumos dalyse“.

A. Puankarė chaoso teoriją aprašė trijų kūnų uždavinio analizėje (Sur le probleme des trois corps et les equations de la dynamique// Acta Mathemaca, vol.13, no.1-2, 1890). Vėliau jis pasiūlė, kad tokie reiškiniai gali būti bendri, pvz., meteorologijoje. V.S. Franklinas⁷⁾ Pierre Duhem’o⁸⁾ veikalo „Traite elementaire de mecanique chimique, fondee sur la thermodynamique“ (2 t. 1897-98) recenzijoje (1898), aptardamas atmosferos jautrumą nežymiems pasikeitimams, pastebėjo (tai vadinamasis „žiogo efektas“): „žiogo stryktelėjimas Montanoje gali nukreipti audrą nuo Filadelfijos į Niujorką“.

¹⁾ Edvardas Lorencas (Edward Norton Lorenz, 1917-2008) – amerikiečių matematikas ir meteorologas, sukūręs teorinį pagrindą oro ir klimato prognozėms bei pagrindą kompiuteriniai atmosferos fizikai ir meteorologijai. Nuo 1955 m. dirbo MIT. Buvo vienu chaoso teorijos pradininkų, sukūrė „Lorenco atraktorių“, įvedė „drugelio efekto“ sąvoką. Skaitmeninėmis oro prognzėmis susidomėjo 6-me dešimtm.; šio dešimtmečio pabaigoje skeptiškai žiūrėjo į tiesinius statistiniu smetodus meteorologijoje, nes dauguma oro reiškinių buvo netiesiniai. 1961 m. naudojo paprastą LGP-30 kompiuterį oro modeliavimui pagal 12-a kintamųjų. Kai panoro „sutaupyti“ ir tęsė simuliaciją nuo vidurio įvesdamas anksčiau atspausdintas reikšmes, jis aptiko, kad jis gauna visai kitokius rezultatus nei paskaičiuoti prieš tai (tai nutiko dėl nežymaus skaičių apvalinimo). Taip jis nustatė, kad nežymūs pakeitimai pradinėse sąlygose gali sukelti didelius pokyčius ilgalaikėje perspektyvoje. 1983 m. gavo Krafordo, o 1991 m. – ir Kyoto premiją.

²⁾ Nortonas Džasteris (Norton Juster, 1929-2021) – rumunų kilmės amerikiečių mokslininkas, architektas ir rašytojas, žinomas knygelėmis vaikams - ypač „Netikra būdelė mokesčiams“ (1961) ir „Taškas ir tiesė“ (1965). Taip pat išleido „Moters vieta: moterys kaimiškos Amerikos praeityje“ (1996) pagal savo patirtį gyvenant fermoje Masačūsetso valst. Buvo Hempšyro koledžo architektūros ir kraštovaizdžio profesorius (1970-1992).

³⁾ Filipas Merilizas (Philip Errol Merilees, 1940-2018) – kanadiečių kilmės fizikas, vėliau dirbęs JAV (Atmosferos tyrimų centre Kolorade, Jūrų tyrimų laboratorijoje Kalifornijoje), prisidėjęs prie atmosferos ir vandenynų dinamikos supratimo. Nagrinėjo srautų, susidarančių iš atsitiktinės turbulencijos chaotiškų modelių struktūrinius modelius (pvz., vadinamuose eksperimentuose su kriaukle). Baigęs karjerą, mėgavosi golfu.

⁴⁾ Duglas Lilis (Douglas K. Lilly, g. 1929 m.) - amerikiečių meteorologas, dirbęs Nacionaliniame atmosferos tyrimų centre (NCAR) Boulderyje, Kolorado valst., kur tyrinėjo atmosferos dinamiką.

⁵⁾ Džordžas Stiuartas (George Rippey Stewart Jr., 1895-1980) – amerikiečių istorikas, toponimikas ir rašytojas. Jo post-apokaliptinis romanas „Žemė gyvuoja“ (1949) gavo IFA premiją. Romane „Audra“ (1941) pagrindinis veikėjas yra pati audra, o meteorologai seka ją Ramiojo vandenyno pakrantėje. Jame yra frazė: „kinas, nusičiaudėjęs Šen-si mieste, gali privesti žmones kasti sniegą Niujorke“. Kituose kūriniuose irgi minimos aplinkos katastrofos, o. „Ne toks turtingas, kaip manote“ (1968) buvo viena pirmųjų esė apie environmentalizmą.

⁶⁾ Haincas Georgas Šusteris (Heinz Georg Schuster, g. 1943 m.) - vokiečių fizikas, Kilio K. Albrechto vardo un-to profesorius (1986-2008). Parašė įvadą į chaoso teoriją (antras leidimas 2008 m.), plačiai naudotą kaip vadovėlis.

⁷⁾ Viljamas Franklinas (William Suddards Franklin, 1863-1930) – amerikiečių elektros inžinierius fizikas. Lehigh’ o un-to (1807-1915), o vėliau MIT (1915-1929) profesorius. Konsultavo „Generic Electric Co“ ir kitas kompanijas. Išleido vadovėlį „Mechanikos elementai“ (1908) bei kitus (neretai pasirodančius kasmet), o taip pat nemažai kitų knygų, kartais su bendraautoriais. Domėjosi daugeliu temų: elastingumu, vibracijomis, elektromagnetizmu, optika, akustika, termodinamika ir skysčių dinamika. Jo publikacijos buvo dažniausiai teorinės, tačiau keli buvo skirti eksperimentiniams darbams. 1898 m. recenzijoje P. Duhemo knygai išsakė keletą paskaitų, kurios artimos šiuolaikinei chaoso teorijai, pvz., „Nestabilios pusiausvyros būsena susidaro kaitinant apatinius atmosferos sluoksnius“ ir „..be galo maža priežastis gali sukelti baigtinį poveikį“, kartu išsakydamas ir „žiogo efektą“. Buvo gamtos mylėtojas ir Parkų komisijos narys. Lehigh‘o upės saloje įsigijo žemės sklypą ir ten įrengė parką, kuris 1916-ais pavadintas jo vardu. Sukūrė ir patentavo karbido dujų žaislinį „Didžiojo sprogimo“ šautuvą ir 1912 m. įsteigė „Gas Cannon“ kompaniją.

⁸⁾ Pjeras Diuhemas (Pierre Maurice Marie Duhem, 1861-1916) – prancūzų fizikas teoretikas ir mokslo istorikas ir filosofas, žinomas darbais apie Viduramžių mokslą. Paryžiaus akademijos narys (nuo 1913 m.). Dirbo termodinamikos, hidrodinamikos ir elastingumo teorijos srityse. Įvedė termodinaminių potencialų sąvoką (1886). Buvo konvencionalizmo šalininku.

⁹⁾ Robertas Mėjus (Robert McCredie May, Baron May of Oxford , 1936-2020) – australų ekologas, kurio darbai skirti rūšių populiacijos dinamikai ir bioįvairovei taikant matematinius metodus. Buvo Londono Karališkosios draugijos prezidentu (2000-05). Nors buvo ateistas, tvirtino, kad religija padeda aplinkos apsaugai. 1996 m. paprašė liautis skyrus Ig Nobelio premijas britų mokslininkams, nes tai gali skatinti visuomenę nerimtai priimti mokslinius tyrinėjimus.

¹⁰⁾ Alberas Libšaberis (Albert Joseph Libchaber, g. 1934 m.) - prancūzų kilmės amerikiečių fizikas, nuo 1994 m. Rokfelerio un-to Niujorke profesorius. Jo pagrindinis indėlis yra į eksperimentinės kietų medžiagų fiziką. Jis pirmasis stebėjo bifurkacijos kaskadą sukeliančią chaosą ir turbulenciją Rayleigh–Benard’o sistemose. Nuo 20 a. paskutinio dešimtmečio jo tyrimai daugiausia lietė biologiją iš fizikos ir dinaminių sistemų chaoso požiūrio taško.

¹¹⁾ Brianas Hantas (Brian Ramon Hunt) - amerikiečių fizikas, Fizikos mokslų ir technologijos inst-to prie Merilando un-to profesorius. Paskelbė daug straipsnių apie dinamines sistemas – nuo fraktalų geometrijos iki mato teorijos begalinių matavimų erdvėse. Paskutiniu metu dėmesį skiria parametrų erdvei dinaminėse sistemose – kaip ir kodėl sistema pasikeičia iš chaotinio judėjimo į periodinius judėjimus ir atgal, kai kinta sistemos parametrai.

¹²⁾ Edvardas Otas (Edward Ott, g. 1941 m.) - amerikiečių fizikas, daugiausia dirbęs chaoso teorijos ir plazmos fizikos srityse. Merilendo un-to profesorius (nuo 1979 m.). Geriausiai žinomas kartu su kolegomis sukurta chaoso valdymo koncepcija (O.G.Y. metodu). Išleido „Chaosą dinaminėse sistemose“ (1993).