Da Vinči matematinė klaidelė  

Leonardas da Vinči neabejotinai genijus, tačiau anglų rašytojas (ir buvęs povandeninio laivo vadas) G. Menzies^*) savo knygoje „1434: įspūdingas kinų laivynas atplaukė į Italiją ir įžiebė Renesansą“ (2008) teigė, kad daugelį idėjų da Vinči nušvilpė iš kinų. Net jei kažkiek ir yra tame tiesos, argi tai sumažina da Vinči kūrybingumą?

O štai olandų matematikas ir menininkas Rinus Roelofs‘as surado klaidelę didžiojo menininko piešinyje. Luca Pacioli (matematiko, dirbusio Milano kunigaikščio rūmuose) paveikslo kairėje pusė kabantis daugiakampis, vadinamas rombikuboktahedronu, yra sudarytas iš lygiakraščių trikampių, kuriuos visada supa kvadratai. L. Pačioli savo knygoje įdėjo da Vinči nupieštą šio daugiakampio iliustraciją, kurioje ir surasta klaida.

Rombikuboktahedronas gali pasitaikyti ir žvaigždės formos figūrose (pieš. žemiau) – jei įdėsime nurodytus išsikišimus ant kiekvieno šoninio paviršiaus, t.y., piramidę su trikampiu ar keturkampiu pagrindu. Tame piešinyje aiškiai matosi, kad raudonos piramidės turi trikampį pagrindą ir kad jas visada supa 6-ios piramidės su keturkampiu pagrindu. Tačiau da Vinči piešinyje (pieš. aukščiau) taip nėra – piramidė apačioje turi keturias briaunas, kai turėtų turėti tik tris. Įtartinos ir apačioje šonuose ir virš jų aukščiau esančios piramidės (ties 3 ir 9 val.), kurios atrodo tarsi turėtų trikampį pagrindą, kai turėtų turėti keturkampį. Atrodo, kad nėra pavaizduotos ir dviejų trikampių piramidžių (ties 8 ir 4 val.) viršūnės.

„Tegu neskaito manęs nesantis matematiku“. L. da Vinčis neturėjo formalaus matematinio išsilavinimo. Tik sulaukęs 40 m. amžiaus, nuo 1497 m. jis aiškinosi matematinius klausimus pas L. Pačiolį ir parengė taisyklingų kūnų piešinių L. Pačioli knygai „Dieviškoji proporcija“ (1509). Tačiau jis įvedė terminą „Aukso pjūvis“ ir jo principus panaudojo savo paveiksluose ir eskizuose, jo piešiniuose daug vienų figūrų „pertekėjimo“ į kitas (kas būdinga topologijai), užsiėmė skysčių tekėjimo klausimais. Savo kūriniuose naudojo tiesinės perspektyvos principus.

Pataisyta da Vinči piešinio versija:

Da Vinči pirmasis nupiešė rombikuboktahedroną spausdintai versijai. Jis teturėjo tik L. Pačioli nurodymus ir turėjo įsivaizduoti, kaip figūra atrodys atspausdinta, ir ją nupiešti. Greičiausia jis neturėjo modelio ar pasidarė paprastesnius jo pavyzdžius iš vytelių ir medinių lentelių. L. Pačiole portrete rombikuboktahedronas atrodo tarsi pagamintas iš stiklo ir todėl turėjo būti gana sunkus. Maža to, jis iki pusės pripiltas vandens. Kaip tokią sunkenybę galėjo išlaikyti plona grandinėlė? Ir kaip stiklo plokštelės galėjo būti sujungtos taip, kad nepraleistų vandens?

Tuo pat metu šviesos atspindžiai modelyje ir ant jo nupiešti puikiai. Tai atrodytų neįmanoma neturint modelio. Deja, netgi nežinome, kas tapė L. Pačioli portretą (jis dažnai priskiriamas venecijiečiui Jacopo de Barbari, tačiau tai nėra patvirtinta).

---

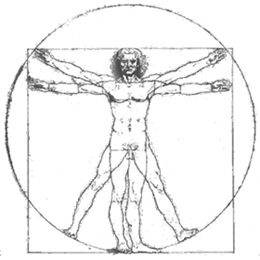
Dar viena nepastebėta forma Vitruvijaus žmoguje?

Leonardo da Vinčio „Vitruvijaus žmogus“ buvo nupieštas 1490-ais – perskaičius romėnų architekto Vitruvijaus raštus. Savo „De architectura“ jis apmąstė idealios žmogaus formos simetriją, nurodydamas bambą kaip centrinį kūno tašką, iš kurio nutįsta visa kita: „jei žmogus guli ant nugaros, … ištiestomis rankomis ir kojomis, o skriestuvu centru imant bambą, jo abiejų rankų ir kojų pirštai lies nuo jos nubrėžto apskritimą“.

Tačiau tai nebuvo vienintelė forma, kuri, Vitruvijaus pastebėjimu, gali tikti žmogaus formai:
„Ir lygiai taip pat, kaip žmogaus kūnas sudaro apskritimo kontūrą, iš jo galima gauti ir kvadratinę figūrą. Jei išmatuosime atstumą nuo pėdų padų iki galvos viršugalvio, o tada pritaikysime tą matavimą ištiestoms rankoms, plotis bus toks pat kaip ir aukštis, kaip ir plokščių paviršių, kurie yra visiškai kvadratiniai, atveju“.

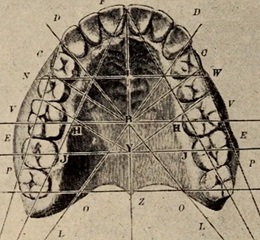
Tačiau neseniai „J. of Mathematics and the Arts“ parodė (2025 m. kovo 28 d. straipsnis), kad tasai Renesanso genijus galėjo savo piešinyje užmaskuoti ir trečiąją formą, kuri iki šiol liko nepastebėta. Jame dantistas Rory Mac Sweeney nurodė, kad tarp Vitruvijaus žmogaus kojų esantis tarpas vaizduoja Bonwill’io trikampį, sudarytą iš apatinio žandikaulio priekinio tarpudančio ir dešiniojo bei kairiojo krūminių dančių galų taškų. William Bonwill’is (1833-1899) 1864 m., ištyręs apie 10 tūkst. dantų, nustatė dantų formos „standartą“.

---

^*) Gevinas Menzis (Rowan Gavin Paton Menzies, g. 1937 m.) – britų rašytojas, buvęs povandeninio laivo vadas, teigęs, kad kinai atplaukė į Ameriką dar iki Kolumbo (1492), tačiau šią idėją istorikai atmetė. Tai jis tvirtino žinomiausiose savo knygoje „1421: kai kinai atrado pasaulį“ (2002). Anot jo tas kinų laivynas po to apiplaukė ir pasaulį iki Magelano (1519-22). Antroje knygoje „1434: ….“ jis išvysto savo hipotezę taikydamas ją Europai (atskiru atveju, kad italai Taccola ir L. da Vinčis savo mechaninių prietaisų iliustracijas paėmė iš 1313 m. Wang Zhen „Knygos apie žemės ūkį), o trečiojoje „Dingusi Atlantidos imperija“ jis tvirtina, kad Atlantida egzistavo Minų civilizacijos pavidalu (žr. Atlantida - tai Kretos sala?).

Erdvės formos
Meilės sinusoidė
Va tai šeimynėlė!
Ar viskas čia taip?
Borchesas ir matematika
Vištų matematiniai pokalbiai
Hipatija – pirmoji matematikė
Papilnėjo da Vinčio kanonas
Tos nepaprastos figūrėlės...
Amerikai matematika nereikalinga!
Meilės ir matematikos ritualai
Šiuolaikiniai iškilūs matematikai
Simpsonų trauka ir žaidimas skaičiais
G. Perelmanas: neįmanoma suprasti keistuolį?
„Da Vinčio kodas", arba Kuo pavojinga virtuali realybė?
Džordžas Birkhofas: matematikas ir meno matuotojas
Australijos aborigenų matematikos samprata
Nėra paprastos visuotinės teorijos!
Leonardo da Vinči kaip neurologas
Omaras Chajamas: ne vien Rubijatai
Matematikos pradžia Lietuvoje
Edgaras Po apie mokslą
Scenoje - paprastos grupės
Išmatuojam apskritimą
Matematiniai anekdotai
Vunderkindo iššūkiai
Gyvenimo gėlelė
Poetinė geometrija
Grandi paradoksas
Pirminiai skaičiai
Vartiklis