Kaip supakuoti standžiau?
Matematikams (Thomas Hales) 2005 m. išsprendus garsųjį rutulių supakavimo uždavinį, kurį dar 1611 m. iškėlė Johanas Kepleris, tai tapo skaniu kąsneliu žiniasklaidai.
|
J. Kepleris spėjo, kad geriausias yra dėjimas į piramidę. Tačiau griežtas įrodymas užėmė 300 puslapių ir jį 4 m. tikrino 12 tikrintojų. Ir net 2005 m. paskelbus žurnale Annals of Mathematics, tikrintojai sakė, kad jie jo teisingumu tikri tik 99%. Tad 2003 m. Th. Halesas pradėjo FlySpeck projektą, kurio tikslas buvo patikrinti įrodymą formalios verifikacijos metodais. Buvo naudota Isabelle ir HOL Light programinė įranga. 2014 m. rugpjūčio 10 d. FlySpeck komanda paskelbė, kad baigė koduoti įrodymo matematinę dalį į
kompiuterinę formą ir patikrino, kad jis neturi klaidų. Taip sudėtingo uždavinio sprendimui buvo panaudotas automatizuotas teoremų įrodymas. |
2009-ais pateikta dar keletas pakavimo problemų sprendimų būdų.
Sukurtas naujas metodas nustatymui, kiek nevienodos formos dalelių galima sutalpinti į
tam tikro dydžio talpą. Tai gali padėti pramonei efektyviau spęsti įvairius pakavimo uždavinius nuo
pardavimo automatų iki vaistų piliulių, kurios būtų mažesnės ir lengviau nuryjamos.
Niujorko universiteto (NYU) Medžiagų tyrimų ir inžinerijos centro fizikai sako, kad sprendimas remiasi kiekiu, nurodančiu su kiek gretimų dalelių liečiamasi. Nors tai atrodo ir intuityviai suprantama, tačiau ilgai nebuvo įrodoma dėl nepaprastai sudėtingos struktūros, kai nagrinėjami netaisyklingos formos ir dydžio trimačiai objektai. Prof. Jasna Brujic2) vadovaujami NYU fizikai sukūrė statistinį modelį, potencialiai leidžiantį išspręsti daugelį pakavimo uždavinių.
Modelis gali nuspėti skirtingų dydžių rutulių talpoje geometriją atsižvelgiant, kiek kaimynų turi vienas rutulys, kaip tie kaimynai yra nutolę ir kaip talpoje pasiskirsčiusi tuščia vieta. Didelės dalelės gali turėti daugiau kaimynų, o mažesnės mažiau. Tokia nuostata derinama su tikimybių teorija.Tai atliekama žvelgiant iš vienos atskiros dalelės taško, todėl jo sukūrėjai jį vadina granocentriniu.
Modelis buvo patikrintas stebint, kaip alyvos lašeliai pasiskirsto vandenyje. Apie tai paskelbta Nature žurnale:
M. Clusel, E.I. Corwin, A.O.N. Siemens, J. Bruji . A 'granocentric' model for random packing of jammed emulsions// Nature, 30 July, 2009
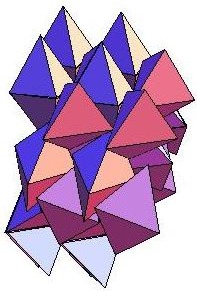
Tuo tarpu Prinstono universiteto chemijos fakulteto prof. S. Torquato ir Mechanikos bei aeroinžinerijos fakulteto studentas Yang Jiao, į nustatytą tūrį supakavo daugiausia tetraedrų (trimatė geometrinė figūra, turinti 4 trikampius šonus) ir kitokius daugiabriaunius. Jie pasiekė 78,2% tūrio užpildymą ir aplenkė prieš metus Mičigano universiteto studentės E. Chen pasiektą rezultatą (77,8%).
Tai jiems pavyko panaudojus naują būdą, kai tetraedrai pakuojami poromis, suglaudus juos briaunomis, besibučiuojančius, ir, žiūrint iš šalies, toks supakavimas atrodo keistai.
Figūrų ir jų derinimas tarpusavyje nėra vien akademinis žaidimas. Pasaulyje pilna jų pradedant apelsinais ir baigiant briaunuotomis smėlio smiltelėmis. Nuo jų tarpusavio išsidėstymo priklauso nemažai procesų, pavyzdžiui, kas vyksta šylant ar šąlant ir t.t. Chemijoje tai susiję su sudėtingų molekulių elgsena vykstant cheminėms reakcijos. Tai turi ir ekonominį efektą pramonėje. Pvz., tai gali leisti į CD įrašyti daugiau informacijos. Mat tai susiję su klaidų aptikimu duomenyse ir automatinių jų koregavimu.
Be praktinių panaudojimų, tai sukuria naujas įžvalgas ir į kitą sritį. Yra 5-i platoniškieji kūnai:
tetraedras,
kubas (heksaedras), oktaedras, dodekaedras ir ikosaedras. Jų simetrija ir grožis tūkstantmečiais žadino
daugelio mąstytojų mintis. Platonas aiškino, kad pagrindiniai elementai (žemė, vėjas, ugnis ir vanduo) yra
sudaryti iš daugiabriaunių. Neolitų laikų daugiabriaunių figūrų rasta Škotijoje.
Plačiau apie briaunainius žr. >>>>>
Tetraedrą standžiausiai supakuoti galima tik suglaudus briaunomis. Tuo tarpu kiti platoniškieji kūnai turi būti pakuojami į gardeles panašiai į apelsinus parduotuvėse eilėmis. kai naujas sluoksnis dedamas į ankstesnė sluoksnio sudarytas įdubas. Mat tetraedras neturi savybės, kuri vadinama centrine simetrija t.y. taško, kuris dalintų pusiau bet kurią atkartą, jungiančią bet kuriuos priešingų šonų taškus. Beje, 12-a Archimedo kūnų (iš 13-os) irgi neturi šios savybės.
Ankstesnės kompiuterinės simuliacijos sudėdavo tetraedrus į virtualią dėžę leisdami jiems augti. S. Torquato adaptyvaus celių susitraukimo optimizavimo algoritmas elgiasi visiškai priešingai jis fiksuoto dydžio virtualius tetraedrus sudeda į dėžę ir ją spaudžia.
Vis tik Prinstono tyrinėtojų išvados nėra iki galo akivaizdžios ir tolimesni teoriniai įrodymai tebėra galimi.
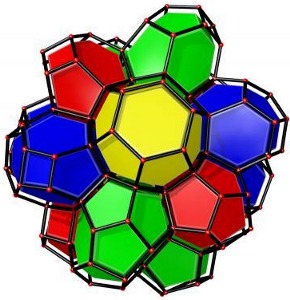
O štai R. Gabbrielli iš Batho universiteto (Anglija, dabar studijuojantis Swansea un-te) sukūrė naują putų modeliavimo būdą, pasiūlęs alternatyvų sprendimą Kelvino uždaviniui. Ir nors jis efektyvumu ir nesumuša Weaire-Phelano struktūros, tačiau parodė naują kelią šio uždavinio tolimesniems sprendimams.
Lordas Kelvinas dar 1887 m. iškėlė klausimą, kaip efektyviausiai padalinti erdvę į vienodo tūrio celes, kad jų paviršius būtų mažiausias. Kelvino sprendimas buvo sutrumpintų oktoedru korys (iš celių, turinčių 6 kvadratinius ir 8 šešiakampius šonus.
Tačiau geresnį sprendimą pasiūlė Dublino Trejybės koledžo fizikai D. Weaire ir R. Phelanas, pasiūlę korį, kurio struktūra įkvėpė Vandens centro architektūrą 2008-ųjų Pekino olimpiadoje. Jį sudarė dvi skirtingos figūros: netaisyklingas penkiakampis dodekaedras (12-os šonų figūra) ir 14-kašonis.
R. Gabbrielli, tirdamas korio formos kaulų pakaitalus, pasiūlė naudoti keturių formų struktūrą. Jo metode naudojama Swift-Hohenbergo dalinių išvestinių diferencialinė lygtis, taikoma dvimačių struktūrų sudarymui. Beje, R. Gabbrielli sudarytos struktūros yra artimesnės natūraliai susidariusioms putoms. R. Gabbrielli buvo pakviestas ir lankėsi JAV bei Australijoje, kur aiškino naująją struktūrą ir ją aptarinėjo su iškiliais matematikais.
Papildomai žr.: S. Torquato, Y. Jiao. Dense packings of the Platonic and Archimedean solids// Nature, Aug 13, 2009, No. 460 (7257)
Taip pat žr. R. Gabbrielli. A new counter-example to Kelvin's conjecture on minimal surfaces// Philosophical Magazine Letters, 2009; 89 (8)
Pakavimas aukštesnių matavimų erdvėse
Erdvėse, kurių matavimas > 3, tankiausias gardelinis pakavimas težinomas tik 8-matei ir 24-matei erdvėms. Maryna Viazovska 2016 m. įrodė, kad E8 gardelė užtikrina tankiausią sferų pakavimą 8-matėje erdvėje (už tai jai 2022 m. paskirtas Fieldso medalis). Vėliau ji ir bendradarbių grupė paskelbė ir panašų įrodymą, kad Leecho gardelė yra optimali 24 matavimui tam buvo remiamasi ankstesniais metodais, parodžiusiais, kad šios dvi gardelės yra labai artimos optimaliam atvejui, kurie buvo jų patobulinti. Kita kryptis aukštesniųjų matavimų srityje yra rasti geresnius tankiausių supakavimų įverčius bet kokiai n-matei erdvei.
Putų tyrimai
Putos jau nuo seno traukė fizikochemikų dėmesį. Pradžioje belgų fizikas Žozefas Plato3) aptiko, kad putos sudarytos ir briaunainių, atskirtų briaunomis-kanalais, užpildytais skysčiu. Po jo savo tyrimus paskelbė britų fizikas ir mechanikas lordas Kelvinas. Sudėtingais skaičiavimais jis parodė, kad putų burbuliukų sudarytas celes galima nagrinėti kaip elementarius briaunainius, kuriais padalijama erdvė. Tas procesas vadinamas grindimu, kurį reikia atlikti taip, kad celių tūris būtų vienodas, o sienelių plotas minimalus. Po šimtmečio 1993 m. airiams Deniui Veirui4) ir Robertui Felanui iš Dublino Trinity koledžo pavyko patikslino Kelvino sprendinį. Jie pasiūlė išgrįsti erdvę 12 ir 14 briaunų briaunainiais.
Tačiau iki šiol neaišku, kodėl vienos medžiagos sukelia putojimą, o kitos ne.
Naujas pakavimo rekordas
Matematika, kaip ir Visata, sklidina tamsiosios materijos...
Matematikoje įverčių gerinimas niekada nesibaigia ir ne išimtis sferų pakavimas daugiamatėje erdvėje. Jis apgaulingas sunkus. 17 a. pradžioje J. Kepleris parodė, kad sudėliojus trimačius rutulius piramide užpildoma apie 74% erdvės. Jis paskelbė, kad tai geriausias išdėstymas tačiau, kad tai būtų įrodyta, prireikė beveik 400 m. (1998 m. Th. Halesas).
O štai aukštesniems matavimas vis dar nežinoma atsakymo ir nuolat pateikinėjami vis tankesni variantai. Ir štai netikėtai ypatingai iki tol nepasižymėjęs Boaz Klartagas5) aplenkė visus ankstesnius įverčius ir manoma, kad jo rezultatas gali būti labai artimas optimaliam. Jo 26 psl. straipsnis pateiktas 2025 m. balandžio 7 d. Tam jis įdarbino seną, tačiau prieš kelis dešimtmečius užmestą techniką. Kartu vėl paaštrėjo senai ginčus keliantis klausimas: optimalus pakavimas yra tvarkingas ar netvarkingas?
1905 m. H. Minkovskis pateikė intuityvų būdą apie
sferų pakavimą: pradedant pasikartojančiu taškų išdėstymu, vadinamu gardele, o tada brėžiant sferą aplink kiekvieną tašką. Šiuo atveju
uždavinys virsta optimalios taškų gardelės suradimu. Pvz., dvimatėje erdvėje optimalia gardele yra taškų išdėstymas šešiakampiu:

Tačiau 1947-ais Claude Ambrose Rogersas6) pasiūlė į uždavinį pažvelgti kitaip.
Pradėkime bet kokia gardele, netgi visai ne optimalia. Tačiau vietoje sferos brėžimo apie tašką brėškime pailgą elipsoidą taip, kad kad jo paviršius
liestųsi su kitais gardelės taškais, bet jų neperžengtų. O tada pasiūlė algoritmą, kaip panaudojant tą elipsoidą gauti tankų pakavimą sferomis:

a) paimti gardelę ir aplink jos tašką nubrėžti elipsę, neleidžiant jai išlysti už kitų gardelės taškų;
b) sutraukti per pusę elipsės ašis išlaikant centrą; c) nukopijuoti elipse užpildant visą gardelę; d) suspausti visą
struktūrą taip, kad elipsės virstų apskritimais; e) gauname tankų supakavimą sferomis.
Rodžerso metodo privalumas buvo tas, kad nereikia pradėti nuo ypač efektyvios gardelės - tereikėjo pasirinkti tinkamą elipsoidą. Tačiau tai sukėlė naują komplikaciją: skirtingai nuo sferos, kurią pilnai apibrėžia vienas skaičius, t.y. jos spindulys, elipsoidą apibrėžia kelios skirtingo ilgio ašys. Kuo aukštesnis matavimas, tuo didesniu skaičiumi skirtingų krypčių galima ištempti elipsoidą ir gauti daugiau variantų pradiniam elipsoidui. Gauname per daug laisvės Todėl matematikai galiausiai sugrįžo prie Minkovskio metodo. Ir nors tai lėmė įvairius pakavimo pagerinimus, tačiau Rodžerso pasiektas lygis buvo pagerintas tik nežymiai. Kad ir kaip ties tuo plūkėsi matematikai, proveržiui reikėjo pašalinio žmogaus!
Žydų matematikas Boazas Klartagas (g. 1978 m.), Veizmano un-to
profesorius, visad domėjosi gardelėmis ir pakavimu, tačiau jam visad trūko laiko į tai rimtai įsigilinti ir tuo užsiimti. Jis daugiausia dirbo
geometrijos srityje, daugiausia su iškilomis formomis, turinčias įvairias simetrijas ir jas laikė ypač galingu matematiniu įrankiu.
2024 m. lapkritį, užbaigęs pagrindinį savo projektą, pasitikrino kalendorių ir pamatė, kad jame nėra svarbių darbų. Ir jis pagalvojo Man 47-eri, visąlaik norėjau tirti gardeles, kodėl to nepadaryti dabar? Ir paprašė draugo Barako Veiso iš Tel Avivo un-to pavadovauti jam. B. Veisas grupelei dalyvių suorganizavo seminarą, kurio metu B. Klartagui pavedė įsigilinti į Minkovskio ir Rodžerso pakavimo būdus.
Ir skaitydamas apie Rodžerso triuką, jis susimąstė, kodėl matematikai užmetė tą metodą. Elipsoidai yra iškilūs, o B. Klartagas mokėjo jais manipuliuoti. Jis pastebėjo, kad pradiniai elipsoidai, kuriuos naudojo Rodžersas, yra intuityvūs, tačiau neefektyvūs. Tad tereikia tik sukonstruoti geresnį elipsoidą.
Jis pradėjo nuo jam žinomo būdo atsitiktinai plečiant ir spaudžiant elipsoido ašis, kol paliesdavo naują gardelės tašką tada ta kryptimi jis sustabdydavo elipsoido plėtimąsi tad kitas gardelės niekada negalėjo patekti į elipsoido vidų. Tačiau elipsoidas plėtėsi kitomis kryptimis, kol vėl nesusiliesdavo su kitu tašku. Tad elipsoidas plėtėsi šuoliukais, vis patyrinėdamas aplinką, kol galiausiai plėstis negalėdavo.
Kadangi Klartago procesas buvo atsitiktinis, kaskart jis gaudavo kitą elipsoidą. Todėl jis įvertino galimų jų tūrių diapazoną. Jam reikėjo rasti didesnio tūrio elipsoidą nei naudojo Rodžersas. Tačiau tai jam nesisekė padaryti. Tad jis kiek patvarkė savo atsitiktinio didinimo procesą ir po kokios savaitės ar dviejų bent kai kuriais atvejais pradėjo gauti didesnio tūrio elipsoidus. Ir apie tai pranešė B. Veisui.
Įrodymas buvo patikrintas. Klartago elipsoidas žymiai pagerino pakavimą. Duotam matavimui d jis leido d kartų pagerinti supakavimo tankį, t.y., pvz., 100-matėje erdvėje jo metodas pakavo 100 kartų geriau. Ir tai jis padarė vos po kelių mėnesių tyrinėjimų ir kelių savaičių rašant įrodymą.
Jo rezultatas atgaivino ir diskusijas apie optimalaus pakavimo prigimtį. Ilgą laiką manyta, kad geriausiu pakavimu yra simetriškos, gardelės principu besiremiantys pakavimai. Tačiau 2023 m. buvo rastas pakavimas neturintis tvarkingos gardelės ir iki Klartago pasiekimo buvęs geriausiu. Tačiau B. Klartagas atstatė status quo, gražindamas viltį, kad simetriškas sprendimas vis tik gali būti teisingas kelias. Vis tik lieka neaišku, ar Klartagas jau buvo per plauką nuo geriausio pakavimo, ar dar yra vietos gerinti pasiekimus.
Atsakymas svarbus potencialiems pritaikymams kriptografijoje ir komunikacijose ir nors pasiekimas nėra betarpiškai dabar naudingas joms, tai padidino entuziazmą.
Kiek yra pasibučiavimų?
Jei vieni pakavimo klausimai pilnai išspręsti, tai vienas paprastas mus palieka aklavietėje; tai Pasibučiavimų skaičiaus uždavinys.
 Bet kokioje talpose kiekviena supakuota sfera turi bučinių kiekį, t.y. susilietimų su kitomis sferomis skaičių.
Atrodo, o kas čia keista?! Supakuotos sferos turi vidutinį bučinių kiekį, kuris leidžia matematiškai apibūdinti padėtį.
Tačiau svarbiausias klausimas lieka neatsakytas.
Bet kokioje talpose kiekviena supakuota sfera turi bučinių kiekį, t.y. susilietimų su kitomis sferomis skaičių.
Atrodo, o kas čia keista?! Supakuotos sferos turi vidutinį bučinių kiekį, kuris leidžia matematiškai apibūdinti padėtį.
Tačiau svarbiausias klausimas lieka neatsakytas.
Pirma pastaba yra dėl matavimų, kurie turi ypatingą prasmę matematikoje: jie yra nepriklausomos koordinačių ašys. X ir y ašys nurodo koordinačių plokštumos du matavimus. Kai fantastiniame filme sako, kad kažkas perėjo į kitą matavimą, tai matematiškai yra nesąmonę, nes neįmanoma pereiti į x ašį.
Vieno matavimo objektas yra tiesė; dviejų matavimų plokštuma. Šiems matavimams nustatytas tikslus pasibučiavimų kiekis. Vienmatėje tiesėje tai 2 (iš kairės ir dešinės), dvimatėje plokštumoje - 6. Įrodymas egzistuoja ir 3D nors jis pasiektas tik 20 a. 6-e dešimtm. (1953 m. K. Schütte ir B. L van der Waerdeno straipsnyje, nors dar Niutonas buvo teisingai nuspėjęs, kad 12). 2003 m. Olegas Musinas įrodė, kad keturmačiu atveju jų yra 24.
O toliau sustota! Tiesa, išskyrus 8 (240) ir 24 (196 560) matavimų atvejus. Kitiems, iki 24-o matavimo, tik nustatytos viršutinės ir apatinės įverčių ribos. Dideliems matavimams ar bendram atvejui klausimas lieka atviras.
|
*) Simpleksinė grupė tai dvi skirtingos, tačiau artimai susijusios grupės. Terminą įvedė Hermann Weyl'as, kad panakintų painiavą ankstesnėje terminijoje (sudėtinga grupė, Abelio grupė). Jis kilęs iš graikiško žodžio, reiškiančio sudėtingas. Simpleksinė vektorinė erdvė yra
vektorinė erdvė V virš lauko F (pvz., realiųjų
skaičių R) su simpleksine bitiesine forma w:VxV -> F. Bitiesinė forma
w yra simpleksinė, jei ji yra: 1) Thomas Callister Hales (g. 1958 m.) - amerikiečių matematikas, dirbantis Langlandso programoje. Jis užsiiminėjo fundamentaliąja lema automorfinių formų teorijoje ir įrodė jos atskirą atvejį Sp(4) simpleksinės grupės*) atveju. Daugelis jo pasiūlytų idėjų buvo panaudotos galutiniam jos įrodymui (Ngo Bao Čau, 2008). Taip pat įrodė Keplerio teiginį, kad sferos tankiausiai išdėliojamos piramidės forma bei korio teiginį (apie paviršiaus suskaidymą vienodo ploto sritimis). Jis daktaro laipsnį gavo Prinstono un-te, profesoriavo Mičigavo, o dabar Pitsburgo un-tuose. Jis pasisako už matematikos formalizavimą ir kompiuterių panaudojimą įrodymų verifikacijai. Inicijavo Flyspeck proektą savo Keplerio pakavimo teiginio įrodymo verifikacijai (užbaigtos 2014 m. rugpjūtį, žr. >>>>>). 2) Jasna Brujic - anglų fizikė, Niujorko un-to profesorė (nuo 2007 m.). Jos tyrimų sritys: eksperimentinė fizika, vienetinės molekulės jėgos spektroskopija, protein mechanika, koloidinių proteinų modelis, streso perdavimas emulsijose 3) Žozefas Plato (Joseph Antoine Ferdinand Plateau, 1801-1883) belgų fizikas, išradęs stroboskopą. 1829 m. plika akimi 25 sek. žiūrėjo į Saulę, norėdamas išsiaiškinti tinklainės atsparumą ir laikinai apako. Aiškinosi persistencijos (regos inercijos) klausimus. Pirmasis atliko bandymą, kai aliejus inde su atskiestu spiritu susirenka į rutulį, kuris nei plaukia, nei skęsta. Jį greitai įsukant, nuo jo atskyla žiedas, kuris savo ruožtu sutrūkinėja, o susidarę rutuliukai suksi aplink pagrindinį rutulį. Jo garbei pavadintas asteroidas 11966. 4) Denis Veiras (Denis Lawrence Weaire, g. 1942 m.) airių fizikas, Dublino Trinity koledžo profesorius. Kartu su savo studentu R. Felanu pateikė kontr-pavyzdį Kelvino teiginiui apie ekonomiškiausią erdvės padalijimą paviršiais su mažiausiu plotu. Jų struktūra buvo panaudota 2008 m. Pekino olimpiados vandens centro dizainui. Šiuo metu dėmesį sutelkė putų struktūros tyrinėjimams ir išleido Putų fiziką (2000, kartu su S. Hutzler) ir Tobulo pakavimo paieškos (2000, kartu su T. Aste), o taip paskelbė kelis straipsnius apie cilindro pakavimą sferomis. Taip pat labai susidomėjęs mokslo istorija ir paskelbęs istorinių esė rinkinius apie airių fizikus. Buvo susijęs su žudiko Ira Einhorn'o byla šį buvo apgyvendinęs savo namuose, o sužinojęs apie JAV pateiktus įtarimus dėl nužudymo, pranešė apie jį FTB. Apie tai pastatytas dokumentinis Interpolo tyrimas (2004), o prieš tai TV filmas Vienaragio žudiko medžioklė (1999). 5) Boazas Klartagas (Bo'az Klartag, g. 1978 m.) - Izraelio matematikas, Veizmano mokslų inst-to Rehomote profesorius. Jo tyrimų sritys: analizė, iškilių formų geometrija, aukštesnių matavimų (jiems artėjant prie begalybės) efektai. Prisidėjo indėliu į asimptotinę geometriją. Yra Journal d'Analyse Mathématique redaktoriumi. 6) Klaudas Rodžersas (Claude Ambrose Rogers, 1920-2005) anglų matematikas, dirbęs matematinės analizės ir geometrijos srityse. Po karo dirbo su H. Davenportu ir per jį susidomėjo pakavimo ir padengimo uždaviniais ir pirmą straipsnį ta tema paskelbė 1950 m., vėliau irgi daug skelbėsi ta tema. Profesoriavo Londono un-to koledže (1958-1986). Skaičių geometrijos srityje jis nustatė ribą tankiam sferų pakavimui. |
Naujas parketo klojimo būdas
Taip pat skaitykite Nauji picos pjaustymo būdai
Vašingtono un-to matematikai rado naują penkiakampio parketo tipą. Iki tol žinota tik 14-a jų, kurių
paskutinis atrastas prieš 30 m.
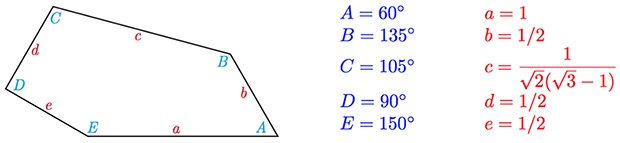
Yra žinoma, kad iškiliais trikampiais ir keturkampiais galima be tarpų iškloti plokštumą, o taip pat, kad yra tik 3-ys tokių šešiakampių tipai (tai įrodyta 1963-ais). O daugiakampiais turinčiais daugiau nei 6 kraštinės, plokštumos iškloti negalima. O kiek yra tai tenkinančių penkiakampių, nėra žinoma.
Pirmą jų klasifikaciją 1918 m. atliko Karenas Reinhardas, aprašęs 5-is figūrų tipus. 1968-85 m. 4-i mokslininkai atrado dar 9-is jų tipus: 1968 m. R. B. Kershneris atrado 3-is, 1975 m. dar vieną atrado R. James. Tada mėgėja M. Rice perskaičius apie R. James atradimą Scientific American susikūrė savo žymėjimo sistemą ir per kelis metus atrado dar 4-is penkiakampius.
Ir štai 2015-ais atrasta 15-a figūra.Ją atrado Casey Mann, Jennifer McLoud ir David Von
Derau, atlikę kompiuterinį variantų perinkimą. Tada Michael Rao 2017-ais parodė, kad ir galimi tik 15-a būdų. Tačiau visi šie
padengimai plokštumą užpildo periodiškai. Nėra žinoma, ar yra nepasikartojantis padengimas.
Galimi padengimai penkiakampiais:

Meilės sinusoidė
Natalia Bielczyk su kitais neuro-matematikais iš Nijmegeno (Olandija) Radboudo universiteto sukūrė matematinį modelį efektyviam bendravimui romantinių santykių atveju, Meilės reikalų dinamika panaši į sinusoidę: vienodas pakilimų ir nusileidimų svyravimas. Kai kurioms poroms šios bangos tampa nekontroliuojamos, sukeliančios nutrūkimą, o kitiems tolygiai nuslopsta į ramybės būklę.
1988 m. Steven Strogatz'as pirmasis aprašė romantinius santykius matematinėmis dinaminėmis sistemomis. Jis sukūrė dvimatį modelį, apibrėžantį du emociškai bendraujančius hipotetinius partnerius. Jis paėmė gerai žinomą Romeo ir Džiuljetos istoriją. Modelis išgarsėjo ir įkvėpė kitus. Tačiau S. Strogatz'o modelis neapėmė pauzių partnerių atsakuose.
Natalia pasiūlė artimesnį gyvenimui modelį, įtraukiant laiko intervalus, būtinus apdoroti ir suformuoti sudėtingą emocinį kompleksą. Atsakas remiasi 4 parametrais: abu partneriai turi asmeninę istoriją (savo praeitį) ir tam tikrus atsaką partneriui ir jo(s) istorijai. Priklausomai nuo šių parametrų, galima nustatyti skirtingas santykių klases: kai kurie pasmerkti santykių nutrūkimui nepriklausomai nuo partnerio skubėjimo, o kiti visąlaik likdavo stabilūs. Paskaičiuotuose modeliuose stabilumas būna, kai abu partneriai pasiekia stabilų pasitenkinimo lygį ir sinusoidė nuslopsta. Straipsnyje daroma išvada, kad plačiai santykių klasei pauzės santykiuose gali padidinti stabilumą poroms. Kurio pradžioje buvo nestabilios.
Šie rezultatai yra gana intuityvūs: pernelyg nekantrūs ar pernelyg vėlyvi atsakai sukelia problemas. Žemiau tam tikros reikšmės, delsimai sukelia nestabilumą, o virš jos jie lemia stabilumą. Tai reiškia, kad tam tikras vangumo lygis gali būti naudingas. Faktas, kad per greitos emocinės reakcijos gali destabilizuoti, rodo, kad kito nuotaikų atspindžiai nepakankami stabiliems santykiams: tam tikra pauzė būtina.
Apibendrinant: straipsnis pateikia matematinį pagrindimą intuityviam socialinės psichologijos reiškiniui. Stebint vienas kito emocijas ir viską darant laiku galima sustiprinti ryšius net nebandant pakeisti partnerio įpročių.
- N. Bielczyk, M. Bodnar, U. Foryś. Delay can stabilize: Love affairs dynamics//. Applied Mathematics and Computation, 2012
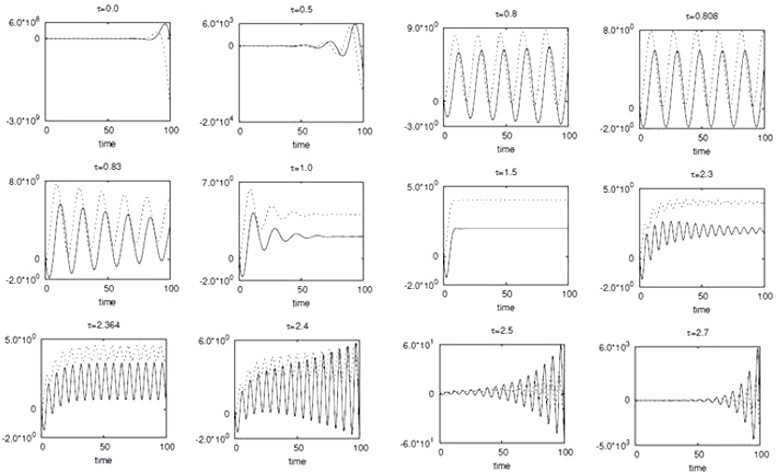 Santykių tarp Romeo (ištisinė linija) ir Džiuljetos (trūki-taškinė linija) modelis. t Žymi atsako užlaikymą. Per trumpos pauzės ( < 0,83) sukelia nestabilumą kaip ir per ilgos pauzės ( > 2,364) |
Krafordo premija
Gyvenimo gėlelė
Kraskalo algoritmas
Matematiniai anekdotai
Žmonės prieš kompiuterius
2018 metai matematikoje
Paviliota senovinio žaidimo
Surasta trilijonas trikampių
Meilės ir matematikos ritualai
Da Vinči matematinė klaidelė
Žaidimų teorijos panaudojimas
Šiuolaikiniai iškilūs matematikai
P-NP: Ant sveiko proto svarstyklių
Kaip įmanomas begalinis klonavimas?
Kaip išgyventi aukštesnius matavimus?
Egzotiškosios hipersferos - problema išspręsta
Klasikinės neišsprendžiamos geometrinės konstrukcijos
Netiesinis mąstymas: išspręsti neišsprendžiamą
Kas per velnias tie pėdai topologijoje?
Geriausios alternatyvos parinkimas
Kelionė į matavimų apibrėžimą
Nepaprasti Visatos skaičiai: 8
Peteris Karvašas. Archimedas
Pirmasis Einšteino įrodymas
Diagramos, pakeitusios pasaulį
Nepaprasti Visatos skaičiai
Revoliucija mazgų teorijoje
Kur viešpatauja chaosas?
Santykis ir proporcija
Kampo trisekcija
Pitagoro teorema
Erdvės formos
Numerologija
Perkoliacija
Vartiklis
 2014 m. naujiena: Kompiuteris patikrino vaisių pakavimo uždavinį
2014 m. naujiena: Kompiuteris patikrino vaisių pakavimo uždavinį