Ferma taškas. Trikampis. Vartiklis

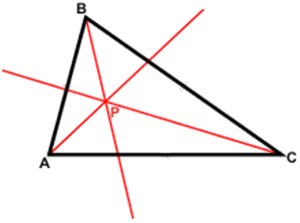
Ferma taškas - tai taškas plokštumoje, nuo kurio bendra visų atstumų iki trikampio viršūnių suma yra mažiausia. Ferma taškas pateikia sprendimą Šteinerio uždaviniui apie minimalaus medžio⁷⁾ sudarymą trikampio viršūnėms.

Tai toks taškas P, kad trikampiui ABC d(P) = |AP|+|BP|+|CP| būtų mažiausias.

Taip jis pavadintas taip todėl, kad tokio taško suradimo uždavinį, kaip iššūkį Evangelistai Toričeliui¹⁾, laiške pateikė P. Ferma. Tasai uždavinį išsprendė panašiu būdu kaip ir Ferma, nors ir panaudojo apie tris trikampius apibrėžtų apskritimų sankirtą. Jo mokinys Viviani²⁾ sprendimą paskelbė 1659 m.

Taškas dar vadinamas ir Toričeli tašku, ypač kontekste, kaip taškas, iš kurio visos trikampio viršūnės matomos 120^o kampu. Toks taškas egzistuoja tik trikampiuose, neturinčiame kampo didesnio už 120^o, be to jis yra vienintelis ir sutampa su Ferma tašku.

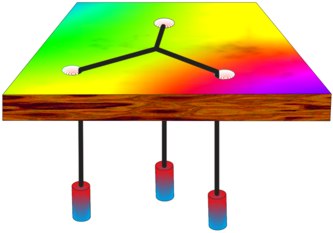
Fiziškai Ferma tašką galima nustatyti taip. Ant plokščio lygaus paviršiaus pažymėkime tris taškus A, B, C ir juose išgręžkime kiauras skyles, Suriškime tris siūlus ir jų laisvus galus prakiškime pro skyles ir prie jų pririškime vienodo svorio svarmenis. Mazgo taškas ir bus Ferma taške.

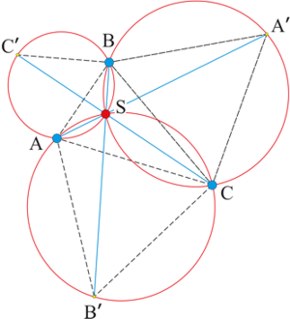
Teorema (E. Toričeli, B. Kavaljeri, T. Simpsono, F. Cheineno, Ž. Bertrano). Ant laisvai pasirinkto trikampio ABC kraštinių į išorę nuo jo nubrėžkime papildomus lygiašonius trikampius ABC‘, BCA‘, CAB‘. Tada šešios kreivės – trys apskritimai, apibrėžti apie tuos trikampius ir tiesės AA‘, BB‘, CC‘ susikerta viename taške S. Jei trikampis ABC neturi kampo, didesnio už 120^o, tada S yra trikampio viduje ir yra Ferma tašku.

Šiuo atveju kampai tarp atkarpų AS, BS ir CS yra lygūs, tad, vadinasi, jie yra lygūs 120^o. Be to, atkarpų AA‘, BB‘ ir CC‘ (vadinamų Simpsono linijomis) ilgiai irgi lygūs ir yra lygūs |AS|+|BS|+|CS|.

Tačiau, jei trikampis turi kampą, didesnį už 120^o, tada susikirtimo taškas S yra už trikampio ribų, o Ferma taškas sutampa su trikampio bukojo kampo viršūne.

Teorema nurodo algoritmą Ferma taško suradimui naudojant liniuotę ir skriestuvą. Tuo netrivialiu atveju, kai trikampis neturi kampo didesnio už 120^o. Ferma taškas randamas kaip bet kurių dviejų apskritimų, nurodytų teoremoje, susikirtimo taškas.
Ferma taško teoremos iliustracija

Kitas būdas surasti Ferma tašką trikampio viduje yra naudoti matematinio optimizavimo metodus, pavyzdžiui Lagranžo daugiklių metodą arba kosinusų teoremą.

Kaip greičiau: tiese ar kreive?

17 a. mokslininkai susidomėjo kreivėmis, kurias brėžia judantys taškai. Tada dar nebuvo bendrų metodų, tad kiekvienu atveju teko atlikti sudėtingus tyrinėjimus. Vienas pirmųjų į tai įsiliejo Galileo Galilėjus, kuris dar 1590 m., nagrinėdamas apskritimo, riedančio tiese, taško trajektoriją, nustatė cikloidę (iš gr. „ratas“) – plokščiąją kreivę, sudarytą iš begalinio skaičiaus arkų. Vienu metu cikloidė buvo labai populiari tarp matematikų: ja tikrino naujus metodus. Vėliau apskritimą „rideno“ kitomis kreivėmis ir nustatė ištisą klasę plokščių kreivių, vadinamų ruletais (iš pranc. roulette - „ratukas“).

1602 m. Galilėjus iškėlė klausimą: kokia greičiausio nusileidimo trajektorija tarp dviejų taškų. Iš pirmio žvilgsnio atrodytų, kad tai tiesė, nes ja atstumas yra trumpiausias. Tačiau tai netiesa.
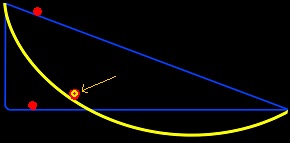Riedėjimo brachistochrone iliustracija Galilėjus galiausiai nusprendė, kad tai apskritimo lankas. Panašią mintį dar anksčiau buvo išsakęs Leonardas da Vinčis, kai nagrinėjo judėjimą nuožulnia plokštuma. Ir abu klydo!

Pirmasis teisingą atsakymą pateikė Johanas Bernulis. Jis 1696-ais metė iššūkį geriausiems to meto matematikams paskelbęs garsųjį uždavinį apie brachistochronę (iš gr. brahiotos - „trumpiausias“ ir hronos - laikas) – taip įmantriai pavadinęs greičiausio nusileidimo kreivę. Sprendimus pasiūlė jo brolis Jakobas³⁾, vokietis G. Leibnicas, prancūzas G. Lopitalis⁴⁾ ir kažkas, panoręs likti nežinomu. Johanas atpažino anonimą („kaip pagal nagus atpažįsta liūtą“, anot lotyniškos patarlės) – I. Niutoną. Šio samprotavimai buvo paprasti ir lakoniški – vos kelios dešimtys žodžių. Pasakoja, kad vos sužinojęs apie uždavinį, jis ėmėsi jį spręsti ir rado atsakymą vos per kelias valandas. Ieškoma kreive buvo apversta cikloidė. Kaip slapta ir jautė J. Bernulis, brachistochronę surado naudojantys naująjį metodą – be galo mažų dydžių skaičiavimą. Tai paaiškina, kodėl Galilėjus nepasinaudojo savo atradimu ir neįžvelgė tokios svarbios cikloidės savybės. O jei ir būtų susipratęs dėl jos, vis tiek nebūtų įstengęs to pagrįsti.

Nepagaunamoji katenarija

Šis klausimas ilgą laiką nedavė ramybės mokslininkams: kokią plokščią kreivę sudaro nuo savo svorio nukarus virvė arba grandinė? Pradžioje manyta, kad parabolę – juk tikrai į ją panašu. Galilėjus netgi siūlė parabolės nubrėžimui ant dviejų vinių pakabinti ploną grandinėlę ir ant sienos pažymėti jos šešėlį. Dekartas tokį metodą laikė klaidingu ir geometriškai nepagrįstu (jis aplamai dažnokai kritikavo garsųjį fiziką, ypač su matematika susijusiais klausimais). Grandine Klaidą pastebėjo ir pats Galilėjus, tame pat brėžinyje pavaizdavęs realiąją grandinę ir parabolės, liečiančios grandinė jos viršūnėje, taškus.

Aptikti neatitikimą buvo paprasčiau nei ištaisyti. Tačiau tai nesutrukdė įvertinti jos panaudojimą architektūroje. 1671 m. anglų fizikas ir išradėjas Robertas Hukas⁵⁾ padarė svarbų atradimą: lygiai tokią pat formą kaip pakabintos grandinės turi, tik apverstą, ir tvirta arka. Tačiau jis nepateikė kreivės aprašymo.

1690 m. Jakobas Bernulis vėl iškėlė uždavinį apie kabojimo kreivę. Be jo, jau kitais metais teisingus sprendimus rado Johanas Bernulis, G. Leibnicas ir olandas Ch. Hiuigensas. Pirmi du pasinaudojo matematine analize, o Ch. Hiuigensas, būdamas klasikinės matematikos šalininku, pasiūlė geometrinį sprendimą, o rastą kreivę pavadino katenarija (iš lot. catena - „grandinė“).

Pirmąkart Ch. Hiuigensas apie šį uždavinį sužinojo iš S. Stevino⁶⁾ mechanikos vadovėlio būdamas 17 m. amžiaus ir netrukus atmetė išvadas dėl parabolės. Kai M. Mersenas paprašė jaunuolį atsiųsti sprendimą, Hiuigensas atsakė, kad nieko nėra parašęs, išskyrus pora teiginių, tačiau vėliau vis tik pateikė nuodugnų geometrinį įrodymą. Tąkart Ch. Hiuigensas parodė ir tai, kad pakabinta grandinė įgauna parabolės formą kai prie jos prikabintas papildomas svoris, vienodai pasiskirstęs per visą ilgį, pvz., drėgna drobė.

¹⁾ Evangelista Toričelis (Evangelista Torricelli, 1608–1647) – italų fizikas ir matematikas, Galilėjaus mokinys, labiausiai žinomas kaip gyvsidabrinio barometro, skirto oro slėgio matavimui, išradėjas, o taip pat darbais optikos srityje. Gabrieliaus ragas

Matematikoje pagarsėjo kaip Toričelio trimito (dažnai vadinamo „Gabrieliaus ragu“), baigtinio tūrio figūros, kurios plotas begalinis, atradimu. Tai tuo metu daugeliui, kaip ir pačiam Toričeliui, atrodė kaip „neįtikėtinas“ paradoksas ir paskatino diskusijas apie begalybės prigimtį. Toričelis taip pat buvo pionierius darbais begalinių eilučių srityje.

²⁾ Vincenco Vivianis (Vincenzo Viviani, 1622-1703) – italų matematikas ir mokslininkas, Toričelio ir Galilėjaus mokinys, pirmosios Galilėjaus biografijos autorius.
1660 m. tiksliau išmatavo garso greitį, 1661 m. tyrinėjo įrenginį, po dviejų šimtmečių gavusį Fuko švytuoklės pavadinimą. Tyrinėjo cikloidę ir parodė, kaip jai nubrėžti liestinę. Įrodė, kad kampo trisekciją galima atlikti panaudojant lygiašonę hiperbolę.

³⁾ Gijomas de Liopitalis (Guillaume Francois Antoine, Marquis de l'Hopital, 1661-1704) – prancūzų matematikas. Parašė darbų iš matematinės analizės, kūgio pjūvių teorijos. Remdamasis Johano Bernulio paskaitomis parašė pirmąją matematinės analizės knygą „Nykstamai mažėjančių dydžių analizė tiriant kreives“, kurioje pateikta funkcijų santykio ribos skaičiavimo taisyklė, kai skaitiklis ir vardiklis artėja prie nulio. Tiesa J. Bernulis pareiškė autorines teises į visą knygą. Kartu su kitais išsprendė brachistochronės uždavinį.

⁴⁾ Jakobas Bernulis (Jacob Bernoulli, 1655-1705) – šveicarų matematikas, vienas iš tikimybių teorijos ir matematinės analizės pradininkų. Jis įrodė atskirą didžiųjų skaičių dėsnio atvejį (Bernulio teoremą). Pirmas jo pasiekimas buvo 1690-ais, kai nustatė kreivės, kuria sunkus taškas leidžiasi per lygius laiko tarpus į vienodus vertikalius atstumus. Tam jis išvedė ir suintegravo dif. lygtį. Kartu buvo pirmąkart įvestas terminas „integralas“. Prisidėjo prie analitinės geometrijos ir variacinio skaičiavimo atsiradimo. Jo vardu pavadinta Bernulio lemniskata. Jis tyrinėjo ir cikloidę, grandinės liniją (apversta cikloidė), o ypač logaritminę spriralę, kurią nurodė pavaizduoti ant paminklo jam. Skaičių teorijoje jo vardu pavadinti Bernulio skaičiai. Pasižymėjo ir kitose matematikos srityse.

⁵⁾ Robertas Hukas (Robert Hooke, 1635-1703) – anglų gamtamokslininkas, pasižymėjęs universalumu. 1660 m. eksperimentais nustatė, o 1676 m. paskelbė Huko dėsnį: „koks ištempimas, tokia jėga“. 1665 m. išleido knygą „Mikrografija“, kurioje pateikė keleto mikroskopinių ir teleskopinių stebėjimų rezultatus bei keletą originalių biologinių pastebėjimų. Jis pirmasis pavartojo biologinį terminą ląstelė (angl. cell), nes augalo ląstelės jam pasirodė panašios į vienuolyno celes. Išrado spiralę laikrodžių varymui, 1684 m. sukūrė optinio telegrafo sistemą, taip pat padarė daugybę kitų išradimų.

⁶⁾ Simonas Stevinas (Simon Stevin arba Stevinus, 1548–1620) – flamandų matematikas, mechanikas ir inžinierius. Išgarsėjo knyga „Dešimtoji“ (De Thiend, 1585), paskatinusi Europoje plačiai naudoti dešimtaines trupmenas. „Aritmetikoje“ jis iracionaliems skaičiams suteikė lygiavertį statusą – apibrėždamas skaičių kaip kažkokios medžiagos matą paskelbiant, kad „vienetas dalomas“ ir nėra jokių iracionalių, neteisingų ir pan. skaičių. Nors ir atsargiai, bet naudojo ir neigiamus skaičius. Apie 1600 m. pademonstravo savo sukonstruotą sausumos jachtą ant ratų – ir ja krantine pravežė princą greičiau nei arkliais. 1586 m. įrodė, kad skirtingos masės daiktai krenta vienodu pagreičiu (tas atradimas dažnai priskiriamas Galilėjui). Išrado dvigubą buhalteriją (debitas-kreditas). Parašė traktatą apie muziką. Vienas pirmųjų pripažino Koperniko heliocentrinę sistemą. Jo garbei pavadintas Mėnulio krateris.

⁷⁾ Šteinerio minimalaus medžio uždavinys iš kombinatorinės optimizacijos srities - surasti trumpiausią tinklą, jungiantį pateiktų neorientuoto grafo taškų rinkinį. Pavadintas J. Šteinerio garbei. Uždavinio ištakos siekia P. Ferma, pasiūliusio (1643): „Duotiems trims taškams rasti ketvirtą, tokį, kad iš jo nubrėžus tris atkarpas į duotus taškus, tų atkarpų suma būtų mažiausia“.
Šteinerio uždavinį galima laikyti dviejų uždavinių kombinatorikoje apibendrinimu: trumpiausio kelio ir minimalaus padengiančio (jungiančiojo) medžio suradimo.