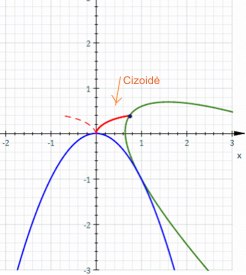
Dioklas ir jo cizoidė
Dioklas (apie 240 m. pr.m.e. - 180 m. pr.m.e.) - graikų geometras, Apolonijaus amžininkas.
[ neretai kai kuriuose straipsniuose jam priskiriami faktai iš gydytojo Dioklo iš Karisto (apie 375-295 m. pr.m.e.) gyvenimo. ]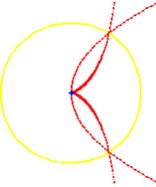
Anksčiau apie jį tebuvo žinoma beveik vien tik iš citatų Eutocijaus komentaruose garsiajam Archimedo veikalui Apie rutulį ir cilindrą. Iš jų buvo aišku, kad Dioklas, spręsdamas kubo padvigubinimo uždavinį, nagrinėjo cizoidę. Taip pat minima jį labai originaliai sprendus Archimedo uždavinį - padalinti rutulį plokštuma taip, kad nukirstų dalių tūriai atitiktų užduotą santykį. Šį uždavinį, susivedantį į kubinės lygties sprendimą, Dioklas sprendė lygiašonės hiperbolės susikirtimo su elipse būdu.
Pateiktos ištraukos iš Dioklo veikalo Apie uždegančius veidrodžius rodo jį buvus pirmuoju, kuris nustatė parabolės formos veidrodžių savybė spindulius nukreipti į židinį (skaitykite apie parabolės savybes). Ir nors vėlesni graikų mokslininkai, iš esmės, ignoravo Dioklo darbus, jie padarė įtaką arabų matematikams, ypač al-Haythamui1),kurio maždaug 1200 m. veikalo vertimas į lotynų kalbą europiečiams grąžino Dioklo nustatytas parabolinių veidrodžių savybes (skaitykite apie galimybę veidrodžiais uždegti laivus).
Tačiau neseniai Irane Mašhado Šrine2) bibliotekoje buvo atrastas Apie uždegančius veidrodžius vertimas į arabų kalbą. 1976 m. jį išvertė, parašė komentarus ir išleido Toomeris3). Iš jo sužinome, kad Zenodoras vyko į Arkadiją6) pokalbiui su Dioklu - tad, be abejonių, kažkuriuo metu Dioklas gyveno Arkadijoje, kuri neatrodė buvus svarbiu matematikos centru, bet heleniškuoju laikotarpiu matematika buvo vystoma ne kultūros centruose įsteigtose mokyklose, o atskirų mokslininkų, išsibarsčiusių visoje Graikijoje. Jie gyvai bendravo tarpusavyje tiek susirašinėdami, tiek aplankydami vieni kitus.
Pitijus, geometras iš Tasoso4), parašė laišką Kononui, klausdamas, kaip surasti veidrodžio paviršių, kad atspindėti Saulės spinduliai sudarytų apskritimą. Ir kai astronomas Zenodoras atvyko į Arkadiją ir buvo priimtas, jis klausė mūsų, kaip rasti veidrodžio paviršių, nuo kurio atspindėti spinduliai sueitų taške ir galėtų uždegti
(Apie uždegančius veidrodžius)Apie uždegančius veidrodžius yra sudarytas iš trijų dalių skirtų trim temoms. Jis galėjo būti esant trijų atskirų knygų rinkiniu. Tos temos: uždegantys veidrodžiai, rutulio padalijimo nustatytu santykiu uždavinys ir kubo padvigubinimas. Viso jame yra 16 teiginių, kurių 3 galėjo būti prijungti vėliau.
Pirmasis apie parabolės židinio savybę, kiti du apie sferinius veidrodžius, 4-5 susiję su parabolės direktrise, 7-8 - Archimedo uždaviniui, 10 - kubo padvigubinimui, 11-12 - kaip įterpti du geometrinius vidurkius tarp poros dydžių naudojant cizoidę ir paskutiniai trys apibendrina kubo padvigubinimo uždavinio sprendimą naudojant cizoidę. Ir kitas dviejų geometrinių vidurkių klausimo nagrinėjimas.
Šiame veikale Dioklas aptaria ir uždavinį, kaip sudaryti veidrodį, kurio atspindėti spinduliai sudarytų pasirinktą kaustikos kreivę bei kaip sukurti veidrodį, kad į židinį kristų spinduliai Saulei judant dangumi. O. Neugebaueris parodė, kad uždavinys neišsprendžiamas Dioklo laikmečio priemonėmis, o Hogendijkas - kad jis galėjo būti išspręstas apytiksliai. Kartu jis spėjo, kad Dioklas atitinkamus samprotavimus galėjo pateikti veikale, bet juos išmetė vėlesni perrašinėtojai.
Nuorodos:
- J.P. Hogendijk, Diocles and the geometry of curved surfaces, Centaurus 28 (3-4) (1985), 169-184.
- O. Neugebauer, Note on Diocles' 'burning mirror', in From ancient omens to statistical mechanics, Acta Hist. Sci. Nat. Med. 39 (Copenhagen, 1987), 37-42.
- G.J. Toomer, Diocles On Burning Mirrors, Sources in the History of Mathematics and the Physical Sciences 1 (New York, 1976).
Parabolės brėžiama kreivė
Dioklo cizoidė
Tai kreivė, kuri nubrėžiama parabolės viršūnės, kai parabolė rieda kita tokia pat parabole.
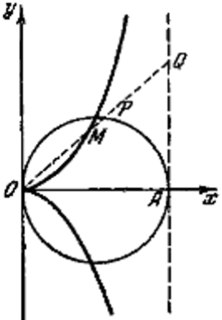
Tai taškų M aibė, kuriems OM=PQ
Lygtis Dekarto koordinačių sistemoje: y2=x3/(2a-x)
Lygtis poliarinėse koordinatėse: r=2a tan(q) sin(q) arba r=a(1/cos(q)-cos(q)
Čia 2a=OACizoidė (reiškianti gebenės formos) įvesta Dioklo (tai nurodoma Archimedo veikale Apie sferą ir cilindrą) apie 180 m. pr.m.e. sprendžiant kubo tūrio padvigubinimo uždavinį. Pavadinimas pirmąkart panaudotas maždaug po 100 m. Gemino5) veikale. Ferma ir Robervalis surado liestinę 1634 m. 1658 m. Ch. Hiugensas ir Wallis nustatė, kad plotas tarp kreivės ir asimptotės yra lygus 3pa2. Iš duoto taško galima nubrėžti vieną arba tris cizoidės liestines.
Dioklo cizoidė yra parabolės viršūnės brėžiama kreivė parabolei riedant tokia pat kita parabole. Niutonas nurodė, kaip nubrėžti cizoidę naudojant dvi statmenas vienodo ilgio atkarpas. Jei jos vedamos taip, kad viena atkarpų visad pereina per fiksuotą tašką, o kitos atkarpos galas slysta tiesia linija, tada slystančios linijos centras brėžia Dioklo cizoidę. Vėliau imta brėžti ne tik apskritimui, bet ir visoms kitoms kreivėms.
Jei cizoidės smaigalys imamas inversijos tašku, cizoidės inversija yra parabolė. Kai spinduliavimo taškas yra (8a, 0), kaustika (atspindžių kreivė) yra kardioidė.
Jei cizoidės taškai P ir Q sujungti su taško O taip, kad jame sudaro statų kampą, tada liestinių taškuose P ir Q susikirtimų taškai yra apskritime, kurio skersmuo (a/2, 0), (2a, 0)
Paaiškinimai
1) Abu Ali al-Hasan ibn al-Haytham (lot. Alhazen, apie 965-1040) arabų mokslininkas universalas, filosofas, matematikas ir astronomas, prisidėjęs prie optikos, astronomijos, matematikos, meteorologijos, vizualinio suvokimo ir mokslinio metodo srityse. Viduramžiais Europoje vadintas Antruoju Ptolemėju arba tiesiog Fiziku. Pagal gimimo vietą kartais vadintas al-Basri, o kartais al-Misri, pažymint, kad atėjo iš Egipto.
Jo vardu vadinamas uždavinys: Duotam šviesos šaltiniui ir sferiniam veidrodžiui, rasti tašką, iš kurio šviesa atsispindi į stebėtojo akį.
Matematikos srityje išvystė analitinę geometriją, sukurdamas ryšį tarp algebros ir geometrijos. Taip pat bandė apskritimo kvadratinimo uždavinį, naudodamas pusmėnulius. Du pusmėnuliai, nubrėžti ant stačiojo trikampio statinių, vadinami Alhazeno pusmėnuliais. Skaičių teorijoje užsiėmė tobulaisiais skaičiais, o taip pat įrodė tai, kas dabar vadinama Vilsono teorema (jei p>1 yra pirminis, tada 1+(p - 1)! yra dalus iš p).
2) Mešhedas miestas šiaurės rytų Irane, netoli Afganistano ir Turkmėnistano, Chorasano provincijos centras. Tai antras pagal gyventojų skaičių miestas Irane (per 3,3 mln.). Yra universitetas. Tai vienas šiitų religinių centrų, šventasis miestas. Buvo vienas iš šilko kelio sustojimų. Jame išlikę XIIXIX a. kulto pastatų: Gauharšado mečetė (XV a.), imamo Rezos mauzoliejus. Netoli Mešhedo yra persų ir tadžikų poeto Firdousi, sukūrusio Šachnamė poemą, kapas.
Mieste yra ir seniausia Vidurio rytų biblioteka, vadinama Astan-e Quds Razavi biblioteka, sauganti per 70 tūkst. retų įvairių laikmečių rankraščių, o taip pat apie 6 mln. istorinių dokumentų.
3) Džeraldas Džeimsas Tumeris (Gerald James Toomer, g. 1934) anglų astronomijos ir matematikos istorikas, parašęs daug knygų apie graikų ir islamo astronomiją. Taip pat į anglų kalbą išvertė Ptolemėjaus Almagestą, o iš arabų Dioklo Apie uždegančius veidrodžius. Profesoriavo privačiame Brauno un-te Rodo saloje.
4) Tasoso sala (Thasos) Graikijos sala Egėjo jūros šiaurinėje dalyje, 12-a sala dydžiu (apie 380 km2, arti 14 tūkst. gyv.). Jau senovėje pasižymėjo įvairiomis kasyklomis (aukso, geležies, vario, brangakmenių. 20 a. pradžioje rasta cinko rūda.
5) Geminas iš Rodo (apie 10 m. per.m.e.-60 m.) graikų filosofas stoikas, matematikas ir astronomas. Išliko jo Įvadas į dangaus reiškinius; iš matematinių veikalų išliko tik kitų cituoti fragmentai (ilgą ištrauką iš Matematikos doktrinos komentaruoje Euklido Elementams pateikė Al-Nayrizi). Pagal Proklą, jis matematiką skirstė į mąstomą ir stebimą (t.y., grynąją ir taikomąją). Pirmajai priskyrė geometriją ir aritmetiką, antrajai mechaniką, astronomiją, optiką, geodeziją, kanoniką (muzikinę harmoniją) ir logistiką (skaičiavimus).
Jo garbei pavadintas krateris Mėnulyje.6) Arkadija istorinė kalnuota Graikijos sritis Peloponeso pusiasalio centrinėje dalyje. Šiuo metu egzistuoja Arkadijos nomas, kurio teritorija iš dalies atitinka senąją Arkadiją. Pavadinimas siejamas su achajų gentimi arkadais ar mitologiniu personažu Arku. 1211 a. pr.m.e. sritis dar nebuvo užimta dorėnų, todėl išlaikė etninį tęstinumą ir senąją Arkadijos-Kipro tarmę, tik ji nebuvo susivienijusi į vieną valstybę ir ją sudarė daugybė kariaujančių polių. 8 a. pr.m.e. Arkadija patyrė kaimyninės Spartos agresiją, neteko kai kurių pietinių sričių, tačiau tai paskatino ją vienytis ir 6 a. ji sustabdė Spartos ekspansiją. Vėliau Arkadijos poliai priklausė Peloponeso lygai ir palaikė Spartą, tačiau vienybės tarp polių šiuo klausimu nebuvo (ypač išsiskyrė Mantinėja). 371 m. pr.m.e. nugalėjus Spartą, poliai, vadovaujant Mantinėjai, įkūrė konfederaciją (Arkadijos lygą) ir pastatė naują sostinę Megalopolį. 362 m. pr.m.e. polių vidiniai konfliktai galiausiai nulėmė lygos subyrėjimą. Netrukus regioną užėmė Makedonija, kuri įjungė jį į Korinto lygą, o 3 a. pabaigoje Arkadijos poliai prisijungė prie Achajos lygos. 146 m. pr.m.e. Arkadija atiteko Romos imperijai.
Nulio istorija
Ferma taškas
Hiparchas iš Rodo
Eudoksas iš Knido
Matematikos keliu
Apolonijus iš Pergo
Parabolės lenktas likimas
Pi keliai ir klystkeliai
Hipokratas iš Chijo salos
Hipatija: pirmoji matematikė
Graikų matematikai: Euklidas
Graikų matematikai - filosofai
Matematikai: Anri Puankarė
Matematika Egipte ir Finikijoje
Matematikos pradžia Lietuvoje
Omaras Chajamas: ne vien Rubijatai
Klasikinės neišsprendžiamos geometrinės konstrukcijos
E. Galua: matematikos genijus ir revoliucionierius
VU Matematikos fakultetas pokariu
Gausas iškirstas langas į 19 a.
Trijų kūnų uždavinys aštuoniukėje
Matematikai: Davidas Hilbertas
Santykis ir proporcija
Senovės graikų astronomai
Pjeras Simonas Laplasas
Kampo trisekcija
Pitagoro teorema
Trikampiai skaičiai
Pirminiai skaičiai
Algebros istorija
Vartiklis