Hiparchas iš Rodo. Vartiklis

Hiparchas iš Rodo (Hipparkhos, apie 190-120 m. pr.m.e.) – graikų matematikas ir astronomas, sudaręs trigonometrines lenteles ir pateikęs metodus uždavinių su sferiniais trikampiais sprendimui. Hiparchas įvedė ilgumos ir platumos sąvokas, iš Babilono perėmė polinę 360^o koordinačių sistemą, 6 min. tikslumu apskaičiavo metų trukmę, sudarė žvaigždėlapį ir manė, kad žvaigždės gali gimti ir mirti.

Manoma, kad Hiparchas gimė Nikėjoje (Bitinijoje, dab. Iznikas, Turkijos Bursa provincijoje), tačiau didžiąją dalį gyvenimo praleido Rodo saloje. 2-3 a. Bitinijoje buvo išleistos monetos jo garbei, kuriose jis vaizduojamas su gaubliu. Vienintelis išlikęs jo kūrinys yra komentarai Arato (3 a. pr.m.e.) poemai apie astronomiją. Kiti jo veikalai (o jų buvo bent 14) apie optiką ir aritmetiką, astronominis kalendorius, geografiniai ir astrologiniai rašiniai, „Apie žemyn svorio tempiamus objektus“ ir kt. neišliko. Daugiausia apie jį žinoma iš Ptolemėjaus „Almagesto“ (2 a.), kuriame gausiai panaudoti Hiparcho darbai. Papildomai nuorodų į jį yra pas Papusą ir Teoną (abu iš Aleksandrijos) jų „Almagesto“ komentaruose, Strabono „Geografijoje“ ir Plinijaus Vyresniojo „Gamtos istorijoje“.

Hiparchas astronomijoje naudojo geometrinius modelius, tame tarpe Apolonijaus (apie 200 m. pr.m.e.) naudotas deferentės epicikliką ir ekscentriką. Vienas jo indėlių – stebėjimais gautų duomenų įtraukimas į geometrinius modelius, todėl G. Toomer‘is jam priskiria trigonometrijos sukūrimą. Hiparchas buvo labai atsidavęs stebėjimams – jo stebėjimų užrašai apima 147-127 m. pr.m.e. Jis naudojo instrumentą, kurį Ptolemėjus apibūdino kaip dioptra ir galėjo būti išradęs planisferinę astroliabiją.

Jis sukūrė teorijas apie Saulės ir Mėnulio judėjimą, parodydamas (kaip sako Ptolemėjas), kad „tai yra vienodas judėjimas apskritimu“. Kartu Ptolemėjas atkreipė dėmesį, kad, kiek žinoma, Hiparchas nesukūrė teorijų dėl 5-ių žinomų planetų. Tačiau jis jas stebėjo ir parodė, kad faktai neatitinka su to meto astronomų hipotezėmis.

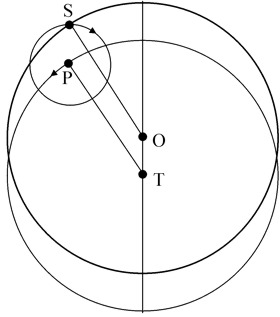Pastebėjo ir lygiadienių pasislinkimą (precesija), o O. Neugebauer‘is spėja, kad iš, faktiškai, sukūrė žemės drebėjimų teoriją.

Ryškus jo sąryšis su Babilono idėjomis. Išskyrus Timocharisą ir Aristilių, jis buvo pirmasis graikas, ėmęs dalinti apskritimą į 360 dalių (prieš jį Eratostenas naudojo paprastesnį dalijimą į 60 dalių). Taip pat jis naudojo Babilono vienetą perčus (kubitą), lygų maždaug 2^o arba 2,5^o. Hiparcho naudotas ilgasis drakoniškasis Mėnulio periodas (5458 mėnesiai = 5923 drakoniškieji mėnesiai) irgi kelis kartus paminimas Babilono užrašuose (tik tai mininčios lentelės yra iš vėlesnio laiko, tad įtaka nėra aiški).

Hiparcho vardu pavadintas krateris Mėnulyje, asteroidas nr. 4000 ir ESA kosminė astrometrijos misija (Hipparcos).

Hiparchas žinomas kaip pirmas matematikas, sudaręs trigonometrijos lentelę, kurios jam reikėjo skaičiuojant Mėnulio ir Saulės orbitų ekscentriškumus. Jis surašė stygos ilgio reikšmes kiekvienam kampui. Jis jas skaičiavo apskritimui, kurio ilgis 21.600, o spindulys (suapvalinus) – 3438. Tokiam apskritimui 1^o lankas lygus 1. Hiparchas stygų ilgius surašė kampams su 7,5^o žingsniu. Pagal Teoną (4 a.), ši lentelė buvo neišlikusiame veikale „Apie linijas apskritime“. Kai kurie tyrinėtojai spėja, kad jos galėjo išlikti Indijos astronominiuose veikaluose, pvz., „Surya Siddhanta“.

Sudarydamas tą stygų lentelę, Hiparchas turėjo naudoti tikslesnę pi reikšmę nei naudota Archimedo, esanti tarp 3 1/7 ir 3 10/71, tikėtina, kad jis naudojo tą pačią, kaip ir Ptolemėjus (3;8:30 – šešiasdešimtainėje sistemoje). Taip pat lentelės sudarymui jis galėjo naudoti Pitagoro teoremą ir teoremą, žinomą Archimedui. Taip pat galėjo išvesti ir naudoti vadinamą Ptolemėjaus teoremą, nes ji įrodyta „Almageste“ (I:10), o vėliau išvystyta L. Karnoto.

Hiparchas taip pat parodo, kad stereografinė projekcija laikosi dėsnių ir ji transformuoja apskritimus sferoje, kurie neina per projekcijos centrą, į apskritimus plokštumoje. Tai yra astroliabijos pagrindas.

Yra keletas požymių, leidžiančių spėti, kad Hiparchas žinojo apie sferinę trigonometriją, nors seniausias išlikęs tekstas apie tai priklauso Menelėjui iš Aleksandrijos (1 a.). Vėliau ją naudojo Ptolemėjus, skaičiuodamas, pvz., patekėjimo ir nusileidimo taškus ekliptikoje arba Mėnulio paralaksą. Tam tikslui Hiparchas galėjo naudotis gaubliu, nuskaitydamas reikšmes nuo koordinačių tinklelio, arba aproksimuodamas reikšmes pagal plokštumos geometriją. Taip pat galėjo pasinaudoti aritmetinėmis chaldėjų išvestomis aproksimacijomis.

Hiparchas tyrinėjo Mėnulio judėjimą ir patvirtino du jo judėjimo periodus, kuriuos chaldėjai tikriausiai jau buvo nustatę anksčiau. Vidutinis sinodinis mėnuo, išreiškiamas kaip 29 d. + 12 val. + 793 / 1080 val. vėliau buvo naudojamas hebrajų (tikėtina, kad paėmus iš Babilono šaltinių). Chaldėjai taip pat žinojo, kad 251 sinodinis mėnuo lygus 269 anomalistiniams mėnesiams. Hiparchas šį periodą praplėtė padaugindamas iš 17, nes po šio intervalo Mėnulis vėl būna toje pačioje platumoje ir jis artimas sveikam metų skaičiui (345). Todėl užtemimai turi kartotis esant beveik vienodoms aplinkybėms. Jų periodas yra (suapvalinus) 126.007 d. ir 1 val.

Hiparchas šiuos paskaičiavimus galėjo patikrinti palygindamas savo meto užtemimus (141 m. sausio 27 d. bei 139 m. lapkričio 26 d.) su užtemimais Babilono užrašuose, padarytuose prieš 345 m.

Senai žinota, kad Mėnulio judėjimas nėra vienodas: jo greitis keičiasi. Toji anomalija kartojasi tam tikru periodu – tai anomalistinis mėnuo. Chaldėjai tai paskaičiavo aritmetiškai ir sudarė lentelę, pateikiančią kasdieninį Mėnulio judėjimą. Tuo tarpu graikai buvo linkę mąstyti geometriniais dangaus modeliais. Apolonijus iš Pergos 3 a. pr.m.e. pabaigoje pasiūlė du modelius Mėnulio ir planetų judėjimui:

Apolonijus parodė, kad tiedu modeliai matematiškai ekvivalentiški, tačiau abu modeliai nebuvo panaudoti praktiškai. Hiparchas buvo pirmasis, kuris pabandė nustatyti tų orbitų santykines proporcijas ir dydžius. Jis sukūrė geometrinį modelį, leidžiantį nustatyti parametrus iš trijų Mėnulio pozicijų tam tikrose anomalijos fazėse. Jis tai padarė atskirai ekscentriniam ir epiciklikų modeliams – tai Ptolemėjus aprašė „Almageste“ (IV:11).

Hiparchas nustatė tropinių metų trukmę, kuri nuo tikrosios tesiskiria tik 6 min.

Dar iki Hiparcho astronomai žinojo, kad metų laikų trukmė skiriasi. Anot Ptolemėjaus, Hiparchas nustatė, kad pavasario trukmė yra 94,5 d., o vasaros trukmė – 92,5 d. Aiškindamas tokį neatitikimą Hiparchas Žemę laikė nesant Saulės orbitos (aplink Žemę) centre. Ekscentriškumo reikšmė buvo 1/24 orbitos spindulio ir tai gana gerai paaiškino regimą Saulės judėjimą.

Hiparchas taip pat bandė nustatyti atstumus iki Mėnulio ir Saulės, o taip pat jų dydžius. Savo rezultatus paskelbė neišlikusioje 2 knygų traktate „Apie dydžius ir atstumus“, kurį mini Papusas ir Teonas. Kaip ir kiti, Hiparchas nustatė, kad Mėnulio dydis kinta, tačiau nepastebėjo Saulės dydžio pokyčių. Jis nustatė, kad esant vidutiniam Mėnulio atstumui, Mėnulio ir Saulės skersmuo yra vienodas.

Kaip ir kiti, jis nustatė, kad Mėnulis turi pastebimą paralaksą, t.y. jis būna nukrypęs nuo paskaičiuotos vietos (žvaigždžių atžvilgiu) – ir tas skirtumas didesnis, kai jis yra arčiau horizonto. Jis žinojo, kad taip yra todėl, kad Mėnulis sukasi aplink Žemės centrą, tačiau stebėtojas juk yra Žemės paviršiuje. Susidaro trikampis, pagal kurį galima paskaičiuoti atstumą iki Mėnulio matuojant Žemės radiusais.

Teonas iš Smyrno rašė, kad pagal Hiparchą, Saulė yra 1880 kartus didesnė už Žemė, o Žemė – 27 kartus didesnė už Mėnulį (tūriais, o ne skersmeniu). Pritaikius geometriją, Saulė yra lygi 2550 Žemės radiusams, o atstumas iki Mėnulio iki 60,5 Žemės radiusų.

Plinijus rašo, kad Hiparchas parodė, kad Mėnulio užtemimai gali įvykti kas 5 mėn., o Saulės užtemimai kas 7 mėn.; kad Saulė gali pasislėpti dukart per 30 dienų, tačiau tai matys skirtingos tautos. Tikslaus užtemimų laiko ir vietų nustatymui reikėjo patikimos Mėnulio teorijos ir teisingo Mėnulio paralakso supratimo, o taip sferinės trigonometrijos žinojimo. Hiparchas buvo pirmasis, sugebėjęs tai padaryti.

Hiparchas astronominiams paskaičiavimams ir stebėjimams naudojo įvairius instrumentus: gnomoną, astroliabiją ir sferą. Be to, Hiparchui priskiriamas keleto instrumentų sukūrimas. Anot Synesius iš Plolomėjaus (4 a.) jis sukūrė pirmąjį astrolabioną, astroliabijos pirmtaką (jį pamini ir Teonas iš Aleksandrijos). Jo pagalba jis galėjo matuoti žvaigždžių geografinę platumą ir laiką. Anksčiau tai buvo daroma dienos metu matuojant gnomono metamą šešėlį arba kilnojamu prietaisu, vadinamu scaphe. Ptolemėjus mini, kad jis naudojo panašų instrumentą kaip ir Hiparchas, kuris vadinamas dioptra, kuriuo matuotas regimas Saulės ir Mėnulio skersmuo. Jį aprašo Papusas bei Proklas – tai 4 pėdų strypas su atžymomis, skyle žiūrėti viename gale ir sklende, kurią galima stumdyti strypu, tiksliai nustatant Saulės ir Mėnulio disko plotį.

Hiparchas stebėjo ir Saulės ekvinokcijas, ką galima darytu su ekvatoriniu žiedu – jo šešėlis krenta ant jo paties, kai Saulė yra pusiaujyje (t.y., viename iš ekvinokcijos taškų ekliptikoje) arba žemiau ar aukščiau priešingos žiedo pusės, kai Saulė yra šiauriau ar piečiau nuo pusiaujo. Ptolemėjus cituoja Hiparcho ekvatorinio žiedo aprašymą, o toliau aprašo savo meto du tokius prietaisus, esančius Aleksandrijoje. Ring

Savo sferinių kampų žinias Hiparchas pritaikė nustatant vietą Žemės paviršiuje. Prieš jį tinklelį jau naudojo Dicaearchus iš Mesanos, tačiau Hiparchas pirmasis panaudojo matematiką nustatant ilgumą ir platumą. Jis parašė trijų knygų neišlikusį veikalą, kritikuojantį Erastoteną iš Sirenės (3 a. pr.m.e.) „Prieš Erastoteno geografiją“. Apie jį žinome iš Strabono, savo ruožtu kritikuojantį Hiparchą savo „Geografijoje“. Jis pasiūlė skirtingų vietų geografines platumas nustatyti Mėnulio užtemimų metu. Mėnulio užtemimas matomas vienu metu pusėje Žemės ir dviejų vietovių platumos skirtumas gali būti nustatomas iš užtemimo pradžios laikų skirtumo.

Vėlesniais metais (matyt, apie 135 m. pr.m.e.) Hiparchas sudarė žvaigždžių katalogą, kurio originalas neišliko, o taip pat sukonstravo dangaus gaublį su žvaigždynais. Iki jo Eudoksas iš Knido (4 a. pr.m.e.) buvo aprašęs žvaigždes ir žvaigždynus dviejose knygose: „Phaenomena“ ir „Arateia“. Pagal jas Aratas parašė poemą, o Hiparchas, savo ruožtu, komentarus Arato poemai – ir tai tėra vienintelis išlikęs jo kūrinys, kuriame yra daugelio žvaigždžių pozicijos ir žvaigždynų patekėjimo, kulminacijos ir nusileidimo laikai, kurie, atrodo, remiasi jo paties stebėjimais.

Be to, Hiparchas žvaigždes skirstė į 6 ryškumo klases – panaši sistema tebenaudojama ir šiais laikais.

Kalifą Omarą paklausus, ką daryti su Aleksandrijos biblioteka, šis atsakęs: „Jei šios bibliotekos knygose kalbama apie Koranui prieštaraujančius dalykus, tai knygos nedoros ir jas reikia sudeginti; jei jose yra tik tie patys pamokymai kaip ir Korane, tai irgi sudeginkite jas, nes jos nereikalingos“.

Trečiasis bibliotekininkas Eratostenas sudarė poetišką, pilną mitologinių personažų, 44 žvaigždynų katalogą, o taip pat pateikė 475 žvaigždžių sąrašą. Hiparchas iš Bitinijos, Ptolemėjaus VII laikais (2 a. pr.m.e.), be kitų dalykų, nustatė atstumą iki Saulės, o taip pat Saulės ir Mėnulio kelius. Matematikos srityje dirbo su kūgiais.

Ptolemėjas perrašė Hiparchą?

„Tu sugebi išmatuoti apskritimą, tu pasakai atstumus tarp žvaigždžių... Tačiau, jei tu toksai žinovas, išmatuok žmogaus sielą! Pasakyk, didi ji, ar niekinga?
Tu žinai, kuri iš linijų yra tiesė, - kam tau tai, jei nežinai tiesaus kelio gyvenime“,
Seneka

Žvaigždžių katalogas „Amagestas“ (2 a.) kelia abejones. Anglų mokslininkas D. Roulenzas įtikinamai parodė, kad 1025-ių žvaigždžių katalogas sudarytas ne Ptolomėjaus stebėjimų pagrindu. Dar 18 a. Ž. d‘Alamberas pastebėjo, kad, jei į katalogą įeina žvaigždės, kurias galima stebėti iš Rodo salos, tai kodėl jame nėra nė vienos žvaigždės, matomos iš Aleksandrijos? Galiausiai, panaudojęs šviesos spindulių lūžimo ir sugėrimo lenteles, D. Roulensas¹⁾ įvertino matomų iš Rodo žvaigždžių stebėjimo tikimybę (90%) ir iš Aleksandrijos (viena milijardinė procento). Tai patvirtina, kad Ptolomėjus tiesiog pakoregavo žvaigždžių padėtį dėl dangaus skliauto kitimo judant Žemei, tačiau net tai padarė nepakankamai tiksliai.

Labai mažai žinoma apie Ptolomėjų, astronomą, kurį daugelį amžių taip gerbė, kad vadino dieviškuoju. Tikrai žinome tik, kad jis gyveno prie Adriano ir Antonijaus, išgarsėjo 130-aisiais ir mirė po 165 m. Pagrindinį savo kūrinį jis kukliai pavadino „Matematiniu rinkiniu arba sintakse“. Arabai gi jį iškėlė, kaip „Didįjį kūrinį: ir tuo vardu („Almagestas“) mes jį žinome.

Jame jis aiškiai išdėstė savo pasaulio sandaros sistemą su daugybe su ja susijusių klausimų; ten pateikiamas ir prietaisų, būtinų tiksliems stebėjimams, aprašymai. Tačiau įsigilinus į turinį Ptolomėjaus šlovė pasirodys abejotina. Kepleris, nenorėdamas klibinti jo autoriteto, pareiškė, kad per 15-a amžių danguje įvyko rimtų permainų. Tačiau Lemonjė²⁾, Lalandas ir Delambras nebuvo tokie santūrūs ir apkaltino Ptolomėjų pritaikius anksčiau gyvenusio Hiparcho stebėjimus.

Per arabų kalbą mus pasiekė kiti Ptolomėjaus kūriniai. Tik iš jo „Optikos“, kurioje pateikta šviesos lūžimo pereinant iš oro į vandenį ir stiklą lentelė, sužinome, kad graikai darė fizikinius bandymus. Tiesa, reikšmės nurodytos klaidingai, tačiau pats principas suvoktas teisingai.

Pradžioje duomenų padirbimą aptiko smalsus poetas ir filosofas Omaras Chajamas, o gerokai vėliau eksperimentiškai patvirtino prancūzų astronomas Žanas Delambrė ir anglų tyrinėtojas D. Roulensas.

Delambrė nusistebėjo, kad į katalogą nepateko virš Aleksandrijos pasirodantys šviesuliai. Jis išvyko į kelionę po Viduržemio jūrą į vietas, kur gyveno antikos mąstytojai, perkasė kalnus medžiagos, tačiau vis tiek nesugebėjo įrodyti lentelių suklastojimo. Visuomenė nenorėjo pripažinti, kad dalį šviesulių galima stebėti tik Rodo saloje, prie kurios Ptolomėjus nebuvo prisiartinęs. Nesvarbu, kad jis tai išdėstė astronomijai skirtame šešiatomyje.

Ir tik Džono Hopkinso un-to profesoriui Robertui Niutonui³⁾, 1977 m. išleidusiam knygą „Klaudijaus Ptolomėjaus nusikaltimai“ pavyko būti išgirstam. Ir tada tenka pripažinti, kad Ptolomėjus padarė nemažai žalos. Ptolomėjaus lentelės, prognozuojant žvaigždžių padėtis, klydo per 6 val. ir 18 min., kas kėlė painiavą paskaičiavimuose ir kliudė tolimesniems tyrinėjimams.

¹⁾ Denisas Roulenzas (Dennis Rawlins, g. 1937 m.) – amerikiečių astronomas ir istorikas, įgavęs skeptiko reputaciją, ypač dėl istorinių tvirtinimų. Daugiausia žinomas kelionės į Šiaurės polių 20 a. pradžioje tyrinėjimų – knygoje „Robertas Peary šiaurės poliuje: faktas ar išmonė“ (1973) tvirtina, kad R. Peary 1909 m. nebuvo šiaurės poliuje. Antroji jo knyga buvo kritinis Tycho Brahės 1598 m. žvaigždžių leidimas, kuriame jis aptiko 10-ies žvaigždžių klaidingas padėtis. Trečioji jo knyga (2000) buvo skirta R. Byrd‘o skrydžiui į šiaurės polių 1926 m.

²⁾ Pieras Lemonjė (Pierre Charles Le Monnier, 1715-1799) – prancūzų astronomas, fizikos dėstytojas. Ištyrė Saturno sukeltas Jupiterio pertubacijas, 5-is dešimtmečius stebėjo Mėnulį, atliko įdomius žemės magnetizmo ir atmosferos elektros tyrimus, nustatė daugelio žvaigždžių padėtis. Jo garbei pavadintas krateris Mėnulyje.

³⁾ Robertas Niutonas (Robert Russell Newton, ) – amerikiečių fizikas, astronomas, mokslo istorikas, išgarsėjęs knyga „Klaudijaus Ptolomėjaus nusikaltimai“ (1977), kurioje, kad „Almageste“ Ptolemėjas pasinaudojo skaičiavimais, o ne tiesioginiais stebėjimais.