Hipokratas iš Chijo. Matematikai. Variklis

Gimė apie 470 m. pr.m.e. Chijo salos¹⁾ (dabart. Khios), mirė apie 410 m. pr.m.e. Jaunystėje užsiėmė prekyba, tačiau jam neypatingai sekėsi, tad atvyko į Atėnus ir tapo žinomu matematiku.

Mokė Atėnuose ir nagrinėjo klasikines skritulio kvadratūros ir kubo tūrio padvigubinimo uždavinius. Kubo padvigubinimui jis nenurodė konkrečios geometrinės konstrukcijos, o suvedė klausimą į dviejų proporcijų suradimą tarp atkarpos a ir kitos, dvigubai ilgesnės, atkarpos (2a). Pažymėjus tas proporcijas x ir y, gausim:
a/x=x/y=y/a iš kur seka x³=2a³
Būtent taip šiais laikais formuluojamas šis uždavinys. Anksčiau bet koks uždavinio sprendimas naudojant proporcijas vadintas mezolabumu.

Buvo puikus geometras, bet kitais aspektais kvailas ir be jumoro jausmo. Sakoma, kad jis dėl savo naivumo prarado didelę sumą pinigų. Jamblichas²⁾ rašė:
„Vienas pitagoriečių neteko turto, ir nutikus tai nelaimei, jis užsidirbdavo pinigų mokydamas geometrijos“.

Iš to spėta iki tol jį buvus pirkliu, bet praradus laivą, atvyko į Atėnus ir greitai padarė pažangą matematikos srityje. Spėjama Atėnuose jį gyvenus maždaug 450-430 m. pr.m.e.

Spręsdamas apskritimo kvadratūros uždavinį jis rado kaip paskaičiuoti „mėnuliukų“ plotą. Tam naudojo savo teoremą, kad dviejų skritulių ploto santykis yra toks pats kaip kvadratų, kurių kraštinė lygi jų spinduliams.

Jis parašė „Geometrijos elementus“, dingusį veikalą, kuris apėmė nemažai to, ką vėliau Euklidas įtraukė į savo „Elementų“ 1 ir 2 knygas. Joje buvo išdėstyti geometriniai kvadratinių lygčių sprendimo būdai ir ankstyvieji integravimo metodai. Proklas, vienas paskutiniųjų didžiųjų graikų filosofų, rašė:
„Hipokratas iš Chijo, paskaičiavęs mėnulio kvadratūrą, buvo pirmasis iš paminėtų, kuris tikrai sudarė ‚Elementus‘...“

Eudemas iš Rodo, Aristotelio mokinys, parašė „Geometrijos istoriją“, kurioje Hiprokratui priskyrė darbus apie mėnulius. Ši istorija irgi neišliko, tačiau Simplicijus iš Kilikijos, rašęs apie 530 m., pacitavo ištrauką „žodis į žodį su keliais papildymais“ iš Euklido „Elementų“, kad būtų aiškesnis tekstas:

„Mėnulių kvadratūra, laikoma priklausančia nepopuliariai teiginių klasei laikant mėnulius turint ryšį su apskritimais, pirmąkart išnagrinėta Hipokrato ir manoma, kad jo aiškinimas yra teisingas. Tad mes ilgiau apsistosime ir juos aprašysime. Jis pradėjo teiginiu (ir pateikė kaip pirmą teoremą reikalingą tam tikslui), kad panašios skritulio nuopjovos yra tokiu pat santykiu tarpusavyje, kaip jų pagrindų kvadratai. Ir jis įrodė iš pradžių, kad kvadratų plotai su kraštine lygia diametrui yra tokiu pat santykiu kaip pačių apskritimų plotai“.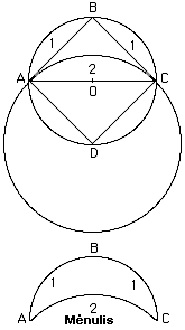

Tai apibūdina „skritulio kvadratūros“ uždavinį - rasti kvadratą, kurio plotas būtų lygus skritulio plotui. Toliau Hipokratas parodė, kaip galime „iškvadratinti“ mėnulio formos skritulio išpjovą.

ABCD yra kvadratas su centru taške O. Nubrėžtų apskritimų centrai yra O ir D (didesniojo). Skritulių nuopjovos, pažymėtos 1 ir 2 remiasi į stačiųjų trikampių įstrižaines (statūs kampai ÐAOB ir ÐADC). Tad jos (1 ir 2) yra panašios. Tad santykiai (pagal teiginį)
Plotas 1 / Plotas 2 = AB² / AC² = 1 / 2
Nes, pagal Pitagoro teoremą, AB² + BC² = AC², o AB = BC, tad AC² = 2 AB²
Tad nuopjovos 2 plotas yra dukart didesnis už nuopjovos 1.

Jei iš pusapskritimio ABC pašalinsime nuopjovą 2, gausime mėnulio formos figūrą, kuriai galime nubrėžti plotą atitinkantį kvadratą. Hipokratas įrodė, kad galima „iškvadratinti“ ir mažesnes ar didesnes už pusapskritimį arkas. Tai buvo nemažas žingsnis bandant rasti apskritimo kvadratūrą (tačiau iš to dar negalima išvesti p reikšmės).

Tikima, nors tiesioginių įrodymų ir nėra, kad Hipokratas panaudojo ir įrodymo neigimo būdu metodą - kai priėmus priešingą prielaidą parodoma, kad ji nėra teisinga.

¹⁾ Chijas - penkta pagal dydį sala Egėjo jūroje prie Mažosios Azijos krantų; per 50 tūkst. gyv. Sala nutįsusi iš šiaurės į pietus per 50 km, o plačiausia vieta siekia 29 km (842 km². Ji yra kalvota, o aukščiausias Pelineono kalnas siekia į 1297 m aukštį. Ji unikali mastika ir Viduramžiškais kaimais. Joje esantis 11 a. Nea Moni priklauso vienuolynas UNESCO Paveldo sąrašui. Chijo saloje atsirado pirmasis Graikijoje vergų turgus.

²⁾ Jamblichas (Iamblichus Chalcidensis, 245-325 m.) – neoplatonikas ir matematikas iš Sirijos, Porfirijaus mokinys, Amapėjos mokyklos vadovas. Buvo Pitagoro biografu. Žinomas „Pitagorininkų teiginių rinkiniu“. Taip pat parašė traktatą „Apie egiptiečių misterijas“ bei komentarus Platono ir Aristotelio veikalams. Išplėtojo Plotino emanacijos koncepciją (padidino būties hipostazių skaičių, dvasios ir sielos hipostazes papildė naujais emanacijos židiniais – dievybėmis, angelais, demonais, herojais). Sielos keliu į Absoliutą laikė ne jo pažinimą, o susiliejimą su juo. Filosofijos sistemą papildė graikų ir Rytų religijos idėjomis, mistifikavo.
Skirtingai nuo Plotino, kuris tvirtino, kad siela nenusileidžia, Jamblichas vėl įtvirtino sielos įsikūnijimą materijoje, tikėdamas, kad materija yra dieviška, kaip ir visas kosmosas.
Savo kosmologijos centre jis patalpino transcendentinį „Aš“, monadą, kurio pagrindinis principas yra protas (nous). Betarpiškai po jo įvedė antrą „Aš“, esantį Absoliuto ir daugio, kaip kaip proto arba sielos (psyche) šaltinį. Tai pradinė diada. Piminis ir aukščiausiasis Aš (nous) yra paskirstytas į supratimo ir proto sferas – pirmoji yra mąstymo sritis, o antroji – mąstymo objektų sritis. Tos trys esybės, psyche ir taip suskirstytas nous sudaro triadą.