Šiame puslapėlyje pradėjome talpinti matematinius tyrimus, turinčius ryšį su kasdieninėmis praktinėmis situacijomis.
Sutramdytas lagaminas

Visi, kurie keliauja, yra susidūrę su nemaloniu reiškiniu, kai tempiamas lagaminas ant ratukų nei iš šio, nei iš to ima šokinėti į kairę ir dešinę, taip ir verždamasis ištrūkti iš rankų, o kartais net ir apsiversdamas, priversdamas skubantį keliautoją stabtelėti.
Prancūzų mokslininkai iš Pari-Didro un-to ėmėsi tirti tą reiškinį. Tam jie sukūrė supaprastintą lagamino modelį ir dėjo ant judančios juostos. Jie nustatė, kad vienam lagamino ratukui susidūrus su kliūtimi, gauna impulsą ir todėl šokteli į viršų, o tada vėl nusileidžia ant žemės. Tačiau pasirodo, kad jis kartu suteikia nežymų postūmį ir antrajam ratukui, kuris irgi savo ruožtu kilsteli aukštyn. O tada nusileidžia ir ... jau supratote? ... suteikia naują postūmį pirmajam ratukui. Ir taip jie pradeda vienas kitą šokdinti. Šiaip, tie šokinėjimai turėtų su laiku nusilpti, tačiau prakeiktas lagaminas ir toliau atkakliai tempiamas ir jam suteikiam energiją, - tad svyravimai stiprėja tiek, kad lagaminas gali apsiversti.
Tada tyrinėtojai ėmėsi nagrinėti, kaip būtų galima sutramdyti nepaklusnų lagaminą. Ir po daugelio bandymo ir klaidų rado. Jie nustatė, kad geriausia tokiais atvejais ... kuo labiau padidinti ėjimą, t.y. tempti lagaminą kuo sparčiau. Mat laiko tarpas tarp kiekvieno ratuko pakilimo ir nusileidimo sutrumpėja, o tai trukdo lagamino siūbavimui. Taip pat bandymai parodė, kad padeda ir lagamino pasvirimo sumažinimas, t.y. prilenkimas prie grindų. Tad jei norime maksimalaus poveikio, tai turim pasilenkti ir tempti lagaminą kuo greičiau. Ir kartu šluostytis prakaitą ir šlovinti mokslą, kuris tai išaiškino.
Greitesnė skaičių daugyba
Skaičių daugyba rūpėjo nuo pat Antikos. Vadinamuoju Babilono būdu pirmojo skaičiaus kiekvienas skaitmuo
sudauginamas su kiekvienu antrojo skaičiaus skaitmeniu. Apie 1956 m. A. Kolmogorovas suformulavo teiginį, kad tai greičiausias įmanomas daugybos būdas: atseit, jei greitesnis būdas egzistuotų, žmonės jį būtų jau atradę (tai yra loginė klaida argumentas iš nežinojimo ir jau po kelių metų paaiškėjo, kad A. Kolmogorovo teiginys klaidingas). Taigi, jis reikalauja N2 operacijų. Taigi, kai abu skaičiai turi po milijardą skaitmenų, reiks atlikti 1018 daugybos operacijų. Jei kompiuteris atlieka milijardą operacijų per sekundę, tokių skaičių sudauginimui jam prireiks 30 m.
1960 m. 23-metis studentas A. Karacuba atrado triuką, leidusį sumažinti operacijų kiekį. O 1971 m. A. Schonhage ir V. Strassenas atrado dar spartesnį daugybos būdą, sumažinantį laiką šiuolaikiniu kompiuteriu iki 30 sek. Savo straipsnyje jie spėjo, kad gali būti dar greitesnis algoritmas.
Ir štai 2007 m. pagaliau M. Fureris įveikė tą ribą ir atvėrė vartus tvanui. Per sekusį dešimtmetį matematikai vis spartino daugybos algoritmą, kaskart per colį artėdami prie N log(N). Ir štai 2019 m. kovą Joris van der Hoevenas ir D. Harvey surado tą algoritmą, pagaliau pasiekę N log(N) įvertį. Jame vietoje vienmačių greitų Furjė transformacijų (GFT), naudotų A. Schonhage-Strasseno algoritme, panaudojamos net 1729-matės GFT. Tiesa, dabartine forma algoritmas nėra praktiškai panaudojamas, tačiau tikimasi, kad jį pavyks išgryninti. Kita vertus, jei Schonhage-Strasseno teiginys, teisingas, tada greitesnio daugybos algoritmo negali būti. Bet visko pasitaiko vėl prisiminkime A. Kolmogorovo atvejį.Daugyba vis spartinama
Visi mes (ko gero?!) mokame sudauginti keliaženklius vadinamuoju stulpelio metodu. Tačiau didelių skaičių dauginimas juo reikalauja atlikti daug veiksmų. Tarkim, reikia paskaičiuoti 314*259. Tam 9-is dauginame iš 4, po to iš 1, o tada iš 3. Tada tą patį darome su 5, o galiausiai ir su 2. Taigi tenka atlikti 9-ias daugybos operacijas. Todėl šis metodas ir vadinamas O(n2) sudėtingumo metodu.
Tačiau 1971-ais Arnold Schönhage ir Volker Strassenas sukūrė greitesnį dauginimo būdą, reikalaujantį O(n * log n * log log n) dvejetainių operacijų. Jis naudoja greitąją Furjė transformaciją. Faktiškai jis yra vieno kintamojo daugianarių daugybos būdas, kai skaičiai išreiškiami daugianariais pagal skaičiavimo sistemos pagrindą, o gavus rezultatą, atliekamas perkėlimas tarp laipsnių. Pvz., dauginame 157 ir 171:
1) 157 atvaizduojame kaip x2+5x+7, o 171 x2+7x+1 (kai x=10);
2) sudauginame tuos daugianarius panaudodami greitąją Furjė transformaciją gaudami x4+12x3+43x2+54x+7;
3) atlikę perkėlimus tarp laipsnių gauname 2x4+6x3+4x+7, kas lygu 26847Schönhage-Strasseno algoritmas taikomas skaičiavimuose su dideliais skaičiais. Tarkim, jei kompiuteris daugintų stulpeliu milijardą skaitmenų turinčius skaičius, jam tai užtruktų kelis mėnesius, tuo tarpu Schönhage-Strasseno metodu jam tereiktų tik 30 sek. Tad jis naudojamas, pvz., Marseno pirminių skaičių paieškai ar Mp skaitmenų radimui, o taip pat kitur, pvz., Lenstra elipsinių kreivių faktorizacijai per Kronekelio sukeitimą. Šis metodas buvo greičiausiu asimptotiškai greičiausiu metodu dideliems skaičiams nuo 1971 m. iki 2007 m., kai Martin Füreris paskelbė dar apie spartesnį algoritmą, tačiau jis labai retai naudojamas. Tačiau vis dar išliko O(n * log n) operacijų siekis, kurį numatė A. Schönhage ir V. Strassenas.
Ir pagaliau 2019 m. David Harvey3) ir Joris van der Hoevenas4) įrodė, kad galimas O(n * log n) daugybos algoritmas, tačiau jis naudoja skaitinius daugiklius, kurie neleidžia jo panaudoti praktiškai. Jis panaudoja naują Gauso perdiskretizacijos techniką, leidžiančią pakeisti daugybą daugiamačių Furjė transformacijų su kompleksiniais skaičiais (skaičiavimo pagrindu 2) rinkiniu.
Prieš policiją pasitelkiant matematiką
Dmitrijus Kriukovas išgarsėjo palyginti neseniai, - ir visai neįprastomis aplinkybėmis. Tai buvo 2012 m. byla dėl ginčytino eismo pažeidimo. Jis ne tai, kad laimėjo bylą neturėdamas advokato, bet ir pateikęs teisėjui analitinę ekspertizę su paskaičiavimais ir grafikais, įrodančią jo nekaltumą.
O viskas prasidėjo taip. Kelių policininkas, budėjęs prie universiteto pastato, nusprendė, kad Kriukovo vairuojama mašina nesustodama pravažiavo ženklą Stop ir Kriukovui buvo išrašyta nemaža bauda. Tačiau pasak Kriukovo, prie ženklo jis sustojo, taisyklių nepažeidė, o policininką suklaidino iškart trijų fizikinių reiškinių sutapimas.
Pirma, Kriukovui artinantis prie Stop ženklo, policininkas įvertino ne mašinos tiesinį, o kampinį greitį. Tai įvyksta kaskart, kai žmonės vertina pro jį judančio objekto greitį ir efektus geriau pastebimas greitai judantiems objektams. Pvz., traukiniai atrodo judantys labai lėtai, kai jie toli, tačiau pro šalį važiuoja labai greitai.
Kriukovo atveju, policininko mašina buvo maždaug 30 m nuo sankryžos su Stop ženklu ant kelio, susikertančio statmenai su pažeidėjo keliu. Tad policininku atrodė, kad prie sankryžos artėjant mašina didina greitį.
Toliau, kai mašina prieš Stop ženklą staigiai stabdoma, tai jos kampinis greitis pradžioje smarkiai didėja, o tada akimirksniu krenta iki nulio. Kriukovas pateikė du grafikus vieną, kai per sankryžą pravažiuojama pastoviu greičiu, o kitą kai mašina staigiai sustabdoma, o tada vėl greitėja, pasiekdama ankstesnį greitį.
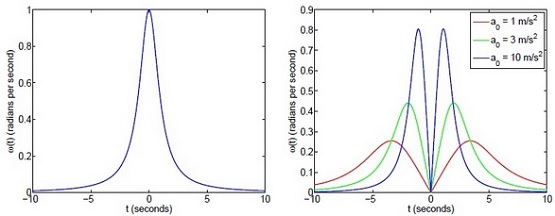
Dešinėje skirtingomis spalvomis pažymėta skirtingų stabdymų pobūdis. Mėlyna linija su aukščiausiais pikais atitinka stabdymą 10 m/sek.2, kas Kriukovo mašinai yra techninis maksimumas. Mat tądien Kriukovas buvo stipriai persišaldęs, pastoviai čiaudėjo, o tai privertė staigiai paspausti stabdžius. Įdomu, kad tasai atvejis išoriškai panašus į esantį kairėje kai mašina pravažiuoja Stop ženklą maždaug 40 km/val. greičiu. Ir ten buvo dar viena mašina, kuri iš dalies užstojo policininko akiratį tad policininkas galėjo ir praleisti tą trumpą sustojimo intervalą.
Ir teisme tie argumentai suveikė. O kai žinia apie neįprastą teismo procesą pasklido po žiniasklaidą, D. Kriukovas patalpino straipsnį Nekaltumo įrodymas į arxiv.org. Tas straipsnis gavo specialų, 400 dolerių prizą.
Aišku, jis nestojo prie to Stop ženklo (užmuškit, - tuo nepatikėsiu) ir po to apsimetinėjo šlangu. Gerai, kad jam pasitaikė juokus suprantantis teisėjas ir to dėka jis išgarsėjo.
Kaip JAV geriausi plaukikai panaudoja matematiką siekdami aukso
2014 m. rudenį Andrew Wilsonas1) sėdėjo pirmame suole Ken Ono paskaitose apie skaičių teoriją Emory un-te Atlantoje. Jis ne tik mokėsi taikomosios matematikos ir fizikos, bet ir buvo un-to plaukimo komandos narys. Jiedu nusprendė suvienyti jėgas, kad padėtų plaukime.
Ken Ono, kuris šiaip tyrinėja abstrakčias skaičių savybes ir specialias funkcijas, kurios vadinamos moduliarinėmis formomis, pradėjo rinkti ir analizuoti A. Vilsono ir kitų plaukikų iš un-to komandos duomenis, kad nustatytų ir įvertintų kiekybiškai jų silpnąsias vietas, kad galima būtų jas pašalinti. Viskas rėmėsi tik Niutono dėsniais ir matematinėmis lygtimis.
Per du metus A. Vilsonas laimėjo universitetų čempionatą ir vyko į 2021 m. Tokijo olimpiadą laimėti aukso medalio. Per tą laiką Ken Ono persikėlė į Virdžinijos un-tą, kur toliau dirbo su Todd DeSorbo, JAV moterų olimpinės plaukimo komandos treneriu ir prisijungė prie komandos kaip konsultantas per Paryžiaus olimpiadą 2024-ais.
Apie jo darbo sėkmę kalba rezultatai. Pasaulio čempionatuose Virdžinijos plaukikės laimėdavo aukso medalius. Iš Paryžiaus olimpiadoje dalyvavo 9-i UVA plaukikai (25% visų JAV plaukikų). Iš jų Kate Douglass2) Paryžiaus olimpiadoje plaukimo krūtine 200 m rungtyje pasiekė JAV rekordą ir laimėjo aukso medalį; kitų rezultatai irgi įspūdingi.
1) Endrie Vilsonas (Andrew Wilson, g. 1993 m.) - amerikiečių plaukikas, 2020 m. olimpiadoje Tokijuje laimėjęs 4x100 m estafetėje aukso medalį plaukdamas krūtine.
2) Keitė Duglas (Katherine Cadwallader Douglass, g. 2001 m.) - amerikiečių plaukikė kompleksinio plaukimo rungtyje, 14 kartų pasaulio čempionė, dukartinė olimpinė čempionė (2024 m.), pasaulio rekordininkė 200 m. laisvu stiliumi ir 200 m kompleksiniu stiliumi trumpajame baseine.
3) Deividas Harvis (David Harvey - australų matematikas, Naujojo Pietų Velso un-to Sidnyje profesorius. Tyrimų sritys: kompiuterinė skaičių teorija ir aritmetinė geometrija, sparti polinominė ir sveikų skaičių aritmetika. Pirmuoju jo svarbesniu pasiekimu buvo dzeta funkcijos hipereliptinei kreivei suradimas (2014). 2019 m., kartu su J. van der Huvenu paskelbė apie greičiausią sveikų skaičių daugybos algoritmą.
4) Joris van der Huvenas (Joris van der Hoeven, g. 1971 m.) - olandų matematikas ir kompiuterininkas, užsiimantis algebrine analize ir kompiuterine algebra. Yra pagrindinis GNU TeXmacs ir Mathemagix sistemų kūrėjas. 2019 m. kartu su D. Harvey paskelbė apie atrastą greičiausią daugybos algoritmą.
Dalyba iš nulio
Apie aukso pjūvį
Kvadratinė lygtis
Zenono paradoksai
Aritmetikos pagrindai
Žvejybos matematika
Kokiu greičiu skriejame?
Kaip supakuoti standžiau?
Parabolės lenktas likimas
Paviliota senovinio žaidimo
Didžiausias bendras daliklis
Iniciatyva: Matematikos keliu
Nepaprasti skaičiai: skaičius 42
Omaras Chajamas: ne vien Rubijatai
Lietaus uždavinys ir matematinis mąstymas
Kai kurie pasiekimai 2020 m. matematikoje: išmazgymas
Kas per velnias tie pėdai topologijoje?
Geriausios alternatyvos parinkimas
Matematikos atgimimas Lietuvoje
Tribologija ir tepimo sprendimai
Galilėjus, Dievas ir Matematika
Vištų matematiniai pokalbiai
Pagaliau: 33 per tris kubus
Didžioji Ferma teorema
Matematika ir biologija
Matematiniai anekdotai
Pitagoro teorema
Nulio istorija
Vartiklis